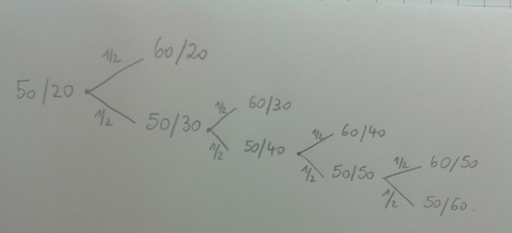Réponse à Pacioli par Bernoulli

[invitec1af6129]

Bonjour,

Voici l'énoncé qui me pose problème :

Une brigade joue à la paume : il faut 60 gagner pour gagner, chaque coup vaut 10. L'enjeu est de 10 ducats. Un incident survient qui force les soldats à interrompre la partie commencée, alors que le premier camp a gagné 50 et le second 20. On demande quelle est la part de l'enjeu qui revient à chaque camp.
Dans ce cas, j'ai trouvé diverses opinions d'un côté comme de l'autre... Mais la vérité et ce que je dirai est la voie droite. Je dis que je peux le faire de trois manières (ici on en donne qu'une)

D'abord on doit considérer combien de manches en plus feront l'un et l'autre camp. Il leur est possible d'en faire 11, c'est à dire lorsqu'ils sont à 50 chacun. Maintenant, je regarde quelle part a de toutes ces manches celui qui a 50, et il en a les 5/11 et celui qui a 20 en a les 2/11. Donc l'un doit prendre pour 5/11 et l'autre pour 2/11, dont la somme fait 7/11. Puis : 7/11 gagne 10 ; qu'est-ce qui revient à 5/11 et 2/11 ? Celui qui a 50 aura 7x1/7 et celui qui a 20 aura 2x6/7

L'objectif des questions qui suivent est de démontrer que la méthode de répartition de Luca Pacioli n'est pas la bonne. On va utiliser les probabilités.

1. Déterminer une épreuve de Bernoulli dans l'expérience aléatoire décrite par Pacioli et donner son paramètre.
2. Construire l'arbre pondéré qui modélise les fins possibles du jeu décrit par Pacioli.
3. Calculer la probabilité que le premier camp gagne la partie puis celle du deuxième camp.
4. Quelle répartition des gains imposent les probabilités ?

Voici déjà ce que je comprends :
Pour gagner, une équipe doit prendre 6 coups.
Sur un match, chaque équipe peut jouer 11 coups.
Est-ce que la question 1 est bien : paramètres (6/11, 1-6/11) ?

Pour le reste, je ne suis pas au niveau, et il faut que j'aide un jeune...
Merci d'avance pour votre aide
Cordialement
-----

[gg0]

Bonjour.

Pour l'éprteuve de Bernoulli, la difficulté est de déterminer la probabilité de gagner de chaque équipe. A 50/50, l'équipe qui a déjà 50 va protester, car elle a déjà montré qu'elle est meilleurs, à 50/20 (5/7 pour l'équipe qui a 50, 2/7 pour l'autre) les perdants vont protester qu'ils ont eu de la chance.
rappel : le jeu de paume, ancêtre du tennis, n'est pas un jeu aléatoire ....

Il y a un souci ici : "Celui qui a 50 aura 7x1/7 et celui qui a 20 aura 2x6/7" Erreur de copie ? Le total de 19/7 ne correspond à rien.

Cordialement.

[invitec1af6129]

Merci beaucoup,

- Alors si je comprends, pour la question 1 la réponse est :
le paramètre c'est (5/7, 2/7)
Et l'épreuve, qu'est-ce que c'est ?

- Comment construit-on l'arbre ? Faut-il en faire 1 pour chaque équipe ?

- Quant au souci, il n'y a pas d'erreur de frappe, c'est bien ça dans le texte et je suis complètement perdue dans tout cet exercice....

Cordialement

[Médiat]

Bonjour,

Construire l'arbre (il n'y en a qu'un) cela consiste à donner l'ensemble des situations possibles à partir d'une situation connue.

La situation connue, ici, est le score 50/20 ; deux événements sont possibles à partir de cette situation, soit la première équipe gagne, soit c'est la deuxième, ce qui donne, soit 60/20 (et le match s'arrête), soit (50, 30) et le match continue.

La pondération consiste à affecter une probabilité à chacune des branches.

[A voir en vidéo sur Futura]

[gg0]

Cet exercice est vraiment bizarre, car Pacioli ne raisonne pas sur un arbre de probabilité, mais apparemment sur de la proportionnalité. On peut effectivement faire un arbre, mais le pondérer ? A part faire 2 branches (A gagne, B gagne) avec les "probabilités" données par Pacioli 5/11, 2/11, ce qui est une arbre bien inutile....

Désolé, mais c'est à l'auteur du sujet qu'il faudrait poser ces questions.

[invitec1af6129]

Merci.

-Alors pour l'arbre est-ce que celui-ci (en pièce jointe) convient ?



-Et la 1ère question ? est-elle bonne ou suis-je dans l'erreur sur la formulation ?

-Et pour la suite je crois que je ne pourrai trouver que si mon arbre est bon...

- "Il y a un souci ici : "Celui qui a 50 aura 7x1/7 et celui qui a 20 aura 2x6/7" Erreur de copie ? Le total de 19/7 ne correspond à rien.
J'ai cherché d'autres énoncés. L'un d'entre eux dit celui qui a 50 aura 7 ducats 1/7 et celui qui a 20 aura 2 ducats 6/7, ce qui pour le coup, fait bien 10 ducats au total...

Merci d'avance pour votre aide !

[gg0]

Pourquoi 1/2 ? Ce n'est pas un jeu aléatoire équilibré, mais un sport.

Le résultat " celui qui a 50 aura 7 ducats 1/7 et celui qui a 20 aura 2 ducats 6/7" correspond à une règle de proportionnalité, avec les coefficients 7/11 et 2/11.

[invitec1af6129]

Je suis complètement perdue.
Mais merci quand même d'y avoir passé du temps !

[Médiat]

Le résultat " celui qui a 50 aura 7 ducats 1/7 et celui qui a 20 aura 2 ducats 6/7" correspond à une règle de proportionnalité, avec les coefficients 7/11 et 2/11.

Ne serait-ce pas plutôt 5/7 et 2/7 (ce qui correspond aux parties jouées) ?

[gg0]

Effectivement,

je raisonne et calcule de travers, aujourd'hui !!

[invitec1af6129]

Alors est-ce que mon arbre est bon ?

[gg0]

Pour une égale probabilité de gagner, oui.
Ce n'est ni dit dans le sujet, ni évident.

Cordialement.

[invite5805c432]

Pacoli dit qu'au vu des 7 précedents matchs, l'issue d'une partie n'est pas equilibré entre les 2 equipes, comme dans l hypothèse de Bernouili classique.

Il evalue que pour chaque manche, une equipe va gagner à 5/7, et une autre va gagner à 2/7. A priori ce sont les parametres demandés dans la question 1.

Ton arbre est correct, mais avec 5/7 et 2/7 au lieu de 1/2 et 1/2. pour la question 2.

pour la question 3, bein tu vois que "l'equipe à 2/11 gagne", correspondra à 2/7*2/7*2/7*2/7 (elle gagne les 4 prochains matchs). ce qui est probablement presque nulle.

ce qui voudrais dire que l'on la quasi totalité de la somme à l'equipe 5/11, et non pas juste les 5/7 comme le dit pacioli.

[invitec1af6129]

Merci !

Pour question 2 :
Est-ce qu'il ne manque pas une branche à partir du dernier 50/60. Car là, il reste une possibilité au 2ème camp pour gagner...

Pour question 3 :
Probabilité que le camp 1 gagne : 5/7
Probabilité que le camp 2 gagne : je ne comprends pas d'où vient le 2/11 ?

Question 4 :
Pourquoi l'équipe 5/11 ?

C'est vraiment complexe !
Et vraiment merci de votre aide !

[gg0]

Ben ... quand il y en a un qui fait 60, il a gagné.

Et ton travail n'est pas de retrouver les résultats de Pacioli, mais de raisonner sur ton arbre.

[invite5805c432]

quand j'ai ecrit Evenement = "l'equipe à 2/11 gagne", ceci sginifie que l'equipe qui était à 2/11, et qui avait besoin de 4 victoires consécutives, à gagné au final...

dans l'arbre de bernouilli que tu as tracé, ceci correspond à à la branche tout en bas qui ce termine par 50/60.

toutes les autres branches correspondent au cas ou c'est l'equipe qui avait l'avantage à gagné.

[invitec1af6129]

Bonjour,

Merci gg0, évidemment, suis-je bête !

Je crois que tout est embrouillé...
3untruc", je comprends de quelle équipe il s'agit mais toujours pas pourquoi le 2/11. Car nous avons inscrit 2/7 sur l'arbre... pour chaque branche inférieure...

Et puis la question 4 ?????

Je suis définitivement perdue

[gg0]

Le 2/11 signifie l'équipe qui avait gagné 2 fois sur les 11 parties possibles (donc 2 fois sur les 7 parties jouées).

[invitec1af6129]

Ah ! Merci !
... Alors l'arbre pondéré, il faut le faire avec le nombre de parties jouées ou le nombre de parties possibles ?

Et question 3, la proba que le 1er camp gagne ? c'est bien 5/7 ?
et la proba que le 2ème camp gagne ? 2/7x2/7x2/7x2/7
Et question 4 ?

[gg0]

Ah ! Merci !
... Alors l'arbre pondéré, il faut le faire avec le nombre de parties jouées ou le nombre de parties possibles ?

On dirait que tu cherches "ce qu'il faut faire" sans t'occuper de la réalité, sans accepter de réfléchir toi-même à la situation, sans vouloir comprendre ce que représente un arbre pondéré.
Je reconnais que le texte qu'on t'a fourni, très confus et probablement mal copié ne t'aide pas. Mais il faut être sérieuse : Tu es dans un exercice de probabilités, il te faut appliquer les règles des probabilités, pas prendre n'importe quel nombre qui est écrit pour faire n'importe quoi.

Du début, je t'ai avertie que le modèle de probabilité est malsain. Untruc t'a proposé de prendre 5/7 et 2/7 et tu l'as suivi (après avoir pris 1/2 et 1/2). C'est comme tu veux, c'est toi qui fais l'exercice (qui ne dit rien sur ce sujet). Mais une fois choisi une règle de probabilité de gain à chaque partie tu t'y tiens, et tu ne viens pas pleurer parce qu'il y a écrit quelque part 2/11.

Et question 3, la proba que le 1er camp gagne ? c'est bien 5/7 ?
et la proba que le 2ème camp gagne ? 2/7x2/7x2/7x2/7

Quelle confusion ! 5/7 est la probabilité de quoi ? exactement, avec tous les mots ? Et 2/7x2/7x2/7x2/7 ?
Inutile de demander des explications si tu ne prends pas le temps de comprendre de quoi il est question : Il y a deux sens ici à "gagne".

Allez, bouge-toi les méninges, on ne peut pas comprendre à ta place, et si tu ne réfléchis pas, nos explications ne te servent à rien. La preuve !

Cordialement.

[invitec1af6129]

Oui, je suis ce que l'un ou l'autre me dit car je ne sais pas qui est dans le vrai.
Je n'arrive pas à savoir nopn plus si je suis sur la bonne piste ou pas...

Alors je vous remercie infiniment d'avoir passé du temps pour m'aider mais à 43 ans, j'ai passé l'âge de me faire engueuler et botter les fesses, surtout quand j'essaie d'avoir des réponses pour aider un jeune souffrant de handicap !... parce que les proba pour moi, c'est un peu loin...

Cordialement

[gg0]

Ben justement,

si tu ne veux pas te faire eng.. ne te contente pas de suivre l'avis de X ou Y, prends tes responsabilités.
Cet énoncé, je l'ai dit dès le début est flou, mal conçu et sans doute faux (erreur de copie). Il n'est pas possible de savoir "ce qui est vrai", l'interprétation de ce qu'il va falloir faire dépend complétement du prof qui l'a posé.

En tout cas, si tu dois aider ce jeune, ne te conduis surtout pas en élève, alors que tu ne l'es pas. N'attends pas qu'on te dise "il faut faire ceci" alors que rien ne permet de décider. par contre, aide ton élève à faire des probas (activité intelligente), à faire fonctionner les règles (donc tu dois aussi les apprendre, ou le laisser faire), pas à copier des corrigés d'exercices sans comprendre.

Cordialement.

NB : j'en ai eng.. des plus vieux que toi, même des plus vieux que moi, qui suis nettement plus âgé que toi. Toujours pour cette même raison : je veux écrire ce qui est juste, pas comprendre.

[invitec1af6129]

Je comprends et il n'est pas question que je recopie une solution sans la comprendre, c'est évident. Mais pour cela il faut que je sache si ce que j'écris est bon.

Oui le sujet est complexe. Ce que j'en comprends, c'est qu'il faut démontrer que le raisonnement de Pacioli n'est pas le bon, en utilisant une épreuve de Bernoulli

Puisque ce jeu n'est pas du hasard, on ne peut pas prendre 1/2. Donc on prend en fonction de la situation au moment où le jeu s'est arrêté. c'est pourquoi, j'ai finalement choisi de mettre 5/7 et 2/7

Question 1 :
Epreuve de Bernoulli : pour chaque manche, le camp 1 gagne à 5/7 et le camp 2 gagne à 2/7,
C'est à dire : (réussite 5/7, échec 1-5/7)
Et on répète n expériences de Bernoulli, c'est à dire 4
Est-ce exact ?

Question 2 :
L'arbre pondéré c'est fait

Question 3 :
Probabilité que le camp 1 gagne : 5/7
Probabilité que le camp 2 gagne (si je suis le chemin) : 2/7 x 2/7 x 2/7 x 2/7
Est-ce exact ? Est-ce bien le bon calcul à faire quand on suis le chemin sur l'arbre pondéré ?

Question 4 :
Je ne comprends pas du tout cette question "Quelle répartition des gains imposent les probabilités ?
Est-ce 5/7 de 10 pour le camp 1 et 2/7 de 10 pour le camp 2 ?

[Médiat]

Bonjour,

Question 3 :
Probabilité que le camp 1 gagne : 5/7
Probabilité que le camp 2 gagne (si je suis le chemin) : 2/7 x 2/7 x 2/7 x 2/7
Est-ce exact ? Est-ce bien le bon calcul à faire quand on suis le chemin sur l'arbre pondéré ?

Un test, qui devrait être un réflexe, avec les probabilités : la probabilité que 1 gagne + la probabilité que 2 gagne ≠ 1 => donc c'est faux !

(Il n'y a pas de match nul)

[invitec1af6129]

OK, parce que ça fait 5/7 + 4/7 = 9/7
Avez-vous, s'il vous plait un indice à me donner pour trouver la bonne solution ?

[invitec1af6129]

Est-ce que mon arbre est faux ?

[Médiat]

L'arbre est correct (sauf les probabilités), mais vous devriez y voir qu'il y a plusieurs chemins (et emprunter un chemin se fait en fonction d'une probabilité) pour que l'équipe 1 gagne.

J'ai l'impresion que votre calcul (message #25) est 2/7 x 2/7 x 2/7 x 2/7 = 4/7, ce qui n'est pas correct ...

Cet exercice met en lumière la traduction en terme de probabilité du "ou" (qui se traduit par un + selon certaines conditions) et du "et" (qui se traduit généralement par un * ), il y a donc du cours à connaître la-dessous ...

[invitec1af6129]

Quest 2 : Proposition d'arbre pondéré. Est-ce que ça vous semble juste ?

50/20
2/7 +----+----+ 5/7
50/30 60/20
3/8 +----+----+ 5/8
50/40 60/30
4/9 +----+----+ 5/9
50/50 60/40
5/10 +----+----+ 5/10
60/50 60/50

Quest 3 : P équipe 2 gagne = 2/7 x 3/8 x 4/9 x 5/10
Qu'en pensez-vous ?

[Médiat]

Ne sachant pas comment vous avez fait vos calculs (pas en suivant mes conseils en tout cas), je ne sais pas où vous vous êtes trompé

[invitec1af6129]

En fait, vous me disiez que l'arbre était bon mais pas les probabilités. j'ai donc réfléchi à nouveau sur les probabilités...

Donc au lieu de laisser chaque "coup" /7, je me suis dis que l'erreur était là, qu'il fallait rajouter une partie à chaque fois
Donc quand on reprend à 50/30, l'une des branches va à 50/40 avec 3/8 probabilités et l'autre branche va à 50/60 avec 5/8 probabilités