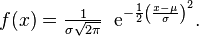Écart-type

[Koranten]

Bonjour,

Petite question "philosophique" concernant l'écart-type.

J'avais gardé en tête qu'il s'agissait de la moyenne des écarts à la moyenne, mais cette définition renvoie en réalité à l'écart-moyen et non pas à l'écart-type.

C'est ce que l'on voit sur cette page Wikipédia :
http://fr.wikipedia.org/wiki/Dispers..._de_la_moyenne

Toujours sur cette page, après la définition de l'écart moyen où l'on est obligé de prendre la valeur absolue pour ne pas avoir un écart moyen bêtement nul, l'écart-type entre en scène. Il est ici "justifié" par le fait que la valeur absolue utilisée par l'écart moyen n'est pas dérivable, ce qui en fait parfois une "impasse" mathématique.

Très bien. On comprend alors le recours à l'élévation au carré plutôt qu'à la valeur absolue. On comprend également bien qu'à la fin, on prenne la racine carré de ce carré, pour avoir une unité (et une valeur) plus, disons, "manipulable".

Mais ce que je ne comprends pas, c'est pourquoi on prend la racine carrée APRES avoir effectué la sommation.

Pourquoi ne pas prendre la racine carrée AVANT la somme ?

Pourquoi ne pas faire la somme de la racine carré du carré ?

En effet, la racine carrée du carré nous renvoie bien ce que l'on voulait : l'écart à la moyenne, sans le signe potentiellement négatif qui nécessitait la valeur absolue pour que l'écart moyen ne soit pas nul.

Et, évidemment, au final, la racine de la somme des carrés ne renvoie pas la même chose que la somme des racines des carrés. Mais pourquoi avoir choisi une formulation plutôt que l'autre ?

Prendre la racine avant de sommer me paraît plus logique, puisqu'en faisant cela on retombe bien sur la même valeur que l'écart-moyen (qui me semble être le point de départ, mais c'est peut-être là que je me trompe : l'écart-type a peut-être d'autres origines théoriques statistiques type régression, khi deux, loi normale, etc. ?)

En quoi la racine de la somme des carrés aurait-elle plus de sens que la racine de la somme des carrés ? Il me semble même que c'est l'inverse.

En quoi mon raisonnement, qui est de dire que l'écart-type devrait renvoyer la même valeur que l'écart moyen, mais sans faire appel à la valeur absolue puisque celle-ci peut poser problème, fait-il fausse route ?

Merci !
-----

[Dynamix]

Salut

Pourquoi ne pas faire la somme de la racine carré du carré ?

Dans ce cas à quoi servirait d' élever au carré ?

La moyenne quadratique des écarts donne plus de poids aux écarts élevés .

[Koranten]

Élever au carré permet d'avoir un écart toujours positif. Sinon, écarts positifs et négatifs s'annuleraient mutuellement.

Prendre la racine du carré permet d'avoir les écarts positifs à la moyenne, puis d'en faire la moyenne.

Ok, la moyenne quadratique donne plus de poids aux écarts élevés. Mais pourquoi voudrait-on leur donner plus de poids?

Ce que je questionne, c'est l'intérêt / la signification de l'écart-type par rapport à l'écart moyen.

Merci !

[Dynamix]

En statistique on cherche les valeurs les plus figuratives d' une population .
L' écart type est plus figuratif que l' écart moyen .

[A voir en vidéo sur Futura]

[Koranten]

J'avoue avoir un peu de mal à voir (à me figurer, si l'on peut dire...) ce que veut dire "figuratif" ici.

Très concrètement, si l'on prend deux exemples :

- des résultats d'élèves à une note de partiel où je veux quantifier ma dispersion
- l'homogénéité d'une solution liquide solide où je veux quantifier la qualité de mon homogénéisation et donc ma dispersion

Je vois (je me figure?) bien dans ces cas là ce que signifie l'écart-moyen. En revanche, je ne vois pas ce que "figure" l'écart-type. En quoi quantifie t-il "mieux" ma dispersion que l'écart-moyen ?

Je ne cherche pas à être bêtement tâtillon, hein, c'est une vraie question que je me pose.

Merci !

[Jerome_sansnumeroderriere]

Les estimateurs, il y en a des tas...
Chacun utilise ceux dont il a besoin.

Dans mon cas, par exemple, j'ai besoin de connaitre une valeur : une masse par pesée, une concentration par dosage, ...
Je répète plusieurs manips.

J'en fais la moyenne et je calcule l'écart-type, la moyenne quadratique des écarts comme tu l'as bien définie.

Je suppose que mes résultats vont suivre une loi normale, ce qui a été observé sauf biais particulier.
Cette loi normale, c'est une gaussienne de formule suivante :



On voit un sigma apparaître et ce sigma, c'est l'ecart type, que tu peux estimer à partir de tes données mesurées.

A partir de là et comme cette fonction est bien connue, tu connais la répartition de tes données et la "chance" d'avoir la valeur vraie dans tel interval.

C'est un peu plus corsé que le niveau collège_lycée après !

[Jerome_sansnumeroderriere]

Pour caractériser une classe et comparer deux populations, deux classes, tu peux aussi utiliser l'écart-moyen, rien ne t'en empêche.. Ecart-type et ecart-moyen te donneront la même indication dans ce cas..

Dans le deuxième cas, homogénéisation de solution, je pense que beaucoup de travail a déjà été fait et qu'une tendance générale dans la répartition a été donnée, non ? Est-ce le cas ?

[Dynamix]

Les estimateurs, il y en a des tas...
Chacun utilise ceux dont il a besoin.

Oui c' est ça l' important .
Un ensemble de données peut être caractérisé par un différents indicateurs :
Moyennes (de toutes sortes) médiane , écart moyen ....
Le choix c' est suivant cas .
Si les données suivent une loi normale , l' écart type s' impose .

[Koranten]

Ok, merci, notamment Jérôme. C'est donc ce que je soupçonnais : c'est lié à la loi normale. C'est une réponse de ce type que j'attendais.

Mais justement, dans mon cas actuel qui est une agitation liquide-solide, ma distribution de concentration dans le volume de ma cuve n'a pas de raison de suivre une loi normale. Pour une cuve relativement homogène oui, et encore, mais dès que c'est stratifié c'est plus normal du tout, c'est asymétrique, déporté d'un côté. Et pourtant dans la littérature de ce genre de choses on croise surtout l'écart-type. J'ai l'impression que c'est plus pour des raisons historiques qu'autre chose, et aussi parce que ça fait le boulot, mais pour moi c'est un cas qui se traiterait plus logiquement avec l'écart moyen.

[gg0]

Bonsoir Koranten.

Si on utilise plus l'écart type que l'écart absolu moyen en statistiques, c'est qu'il est lié aux possibilités de calculer : formules (plus précisément concernant la variance), modélisation probabiliste.
Par exemple, sur une valeur "calculée" par une série d'essais, donc une moyenne d'une série de valeurs, on peut, avec l'écart type, déterminer un intervalle de confiance sur cette valeur (moyenne), à condition d'avoir suffisamment de valeurs (ou même avec peu si la mesure a une dispersion gaussienne). Rien de tel avec l'écart absolu moyen.

Mais rien ne t'interdit d'utiliser l'écart absolu moyen (il est d'ailleurs dans les normes AFNOR de statistiques). par contre, pas moyen de calculer l'écart de l'ensemble de deux échantillons de mesures à partir de celui de chacun des échantillons, de leurs moyennes et de leurs tailles. Ce qui est possible avec l'écart type.

Cordialement.

[Koranten]

Ok, merci.