Bonjour,
je voudrais savoir plus sur cela :
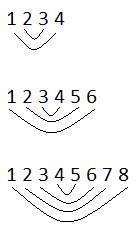
2 + 3 = 5
1 + 4 = 5
----------
3 + 4 = 7
2 + 5 = 7
1 + 6 = 7
----------
4 + 5 = 9
3 + 6 = 9
2 + 7 = 9
1 + 8 = 9
pourquoi quand on prend pour sommer deux nombre comme ça, il en résulte toujours pareil ? pourquoi en ajoutant 2 chifre a la séquence la somme augmente 2 ?
pourquoi cela marche si bien ? il y en a une formalisation ? comment on représente cela ? etc ...
Bonjour.
Simplement, d'une ligne à l'autre, tu ajoutes 1 au premier nombre et tu soustrais 1 au deuxième. Donc le total ne varie pas.
Ça marche non seulement pour les premiers entiers, mais aussi pour toute suite d'entiers successifs. Plus généralement, pour toute suite géométrique.
Pourquoi ça a augmenté de 2 d'une fois sur l'autre : parce que tu ajoutes à 1 un nombre qui fait 2 de plus.
Cordialement.
NB : Gauss, à l'âge de 10 ans, s'en est servi pour donner la somme des nombres de 1 à 100 en très peu de temps. A la surprise de son instituteur.
Plus intéressant encore : la somme de deux chiffres donne le chiffre suivant dans la liste.Envoyé par contanu
Formalisons un peu : On prend les nombres de 1 à n-1, et on les regroupe comme tu l'a fait. Alors on remarque que le k-ième nombre (égal à k) est regroupé avec le nombre n-k, leur somme fait donc k+(n-k)=n, et ce, quelque soit k.
Pour remarquer que k et n-k sont regroupés ensemble, il suffit de remarquer que n-k est le k-ième nombre avant la fin et qu'on le groupe avec le k-ième nombre en partant du début
Cette idée permet de calculer simplement la somme des n premiers entiers, et ce quelque soit n
Vous prenez une série de 1 à n
1, 2 ,3, …p……… n-1, n
Le premier + le dernier c’set 1 + n
Ensuite le deuxième et l’avant d’renier 2 + (n-1) = 1+n
…..
Vous arrivez à p et vous faite p + (n- (p-1)) = 1+n
Ca , je pense, c’est une description mathématique p + (n- (p-1)) = 1+n
merci les gars
je commence a penser a vous reponses
mais comment on formalise gg0? les autres formalisations sont-elles correcte? je crois pas, peut-etre que je n'ai pas encore compris...
c'est possible de parler de cela en termes de progression?
il y a quelqu'un?
Qu'appelles-tu formaliser ? Si c'est écrire des formules, vois des cours sur les suites arithmétiques et la notation.
mais est-ce utile ?
Bon, ce n'est pas la peine de t'aider si tu discrédites les intervenants sans comprendre.
à quelle formalisation fais tu référence.
si tu prends la somme de 1 à n
tu vois bien que que tu peux additionner le premier et le dernier
soit 1+n
qui vaut la même chose que le second et l'avant denier
2+(n-1)= n+1
donc sur la moitié de la somme tu as une succession de (n+1) donc fois n
mais divisé par 2 puisque tu as regroupé les termes deux à deux.
d'ou n(n+1)/2
et si le nb n est impair tu retrouves la même formule
mais je te laisse faire.
mais tu sors cette "haine" d'ou gg0? lisez de nouveau la phrase, il y a la un ENCORE!
cela vaut dire que je suis ENCORE en train de reflechir...
l'ansset a ete plus clair, merci...
si j'ai bien compris l'idee est la suivante:
1 + k
2 + k-1
3 + k-2
n + k-(n-1)
e la raison entre chaque somme est : n(n+1)/2
ça c'est deja formaliser ou manque le pas du raisonnement par recurrence?
je fais des progres
1, 2, 3, 4
1 + k = x
2 + k-1 = x
1, 2, 3, 4, 5, 6
1 + k = x + 2
2 + k-1 = x + 2
3 + k-2 = x + 2
1, 2, 3, 4, 5, 6, 7, 8
1 + k = x + 4
2 + k-1 = x + 4
3 + k-2 = x + 4
4 + k-3 = x + 4
1, 2, 3, 4, 5, 6, 7, 8, 9, 10
1 + k = x + 8
2 + k-1 = x + 8
3 + k-2 = x + 8
4 + k-3 = x + 8
5 + k-4 = x + 8
dans ce cas la le pas du raisonnement par recurrence doit etre fais pour chaque serie et non comme dans mon post antecedant, correcte?
j'ai fais encore plus de progres... mais je me suis arrete la, qu'est-ce que je fais maintenant?
1, 2, 3, 4
1 + 4 = 5
2 + 3 = 5
n = 2
1 => n-1 = 2n
2 => n = 2n -1
______________
1, 2, 3, 4, 5, 6
1 + 6 = 7
2 + 5 = 7
3 + 4 = 7
n = 3
1 => n-2 = 2n
2 => n-1 = 2n -1
3 => n = 2n-2
_______________
1, 2, 3, 4, 5, 6, 7, 8
1 + 8 = 9
2 + 7 = 9
3 + 6 = 9
4 + 5 = 9
n = 4
1 => n-3 = 2n
2 => n-2 = 2n-1
3 => n-1 = 2n-2
4 => n = 2n-3
etc
c'est pour moi incompréhensible.
que veulent dire tes => par exemple ?
