Produit scalaire et maximum

[lper]

Bonjour,

j ai un petit problème sur un exercice de math à résoudre, merci d'avance de votre aide.

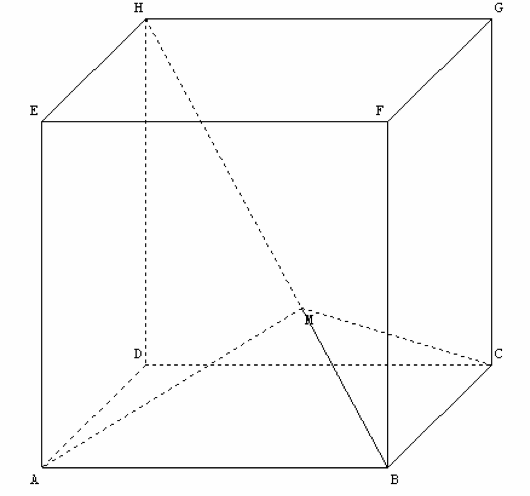
Soit un cube d'arête a et de sommet ABCDEFGH. M est un point de la grande diagonale {BH}. On veut déterminer la position M sur {BH} pour que l'angle AMC soit maximal.
1.Montrer que MA=MC et que scalaire(MA).scalaire(MC)=MA^2 - a^2 -> ok
2.En déduire que cos(AMC) = 1-a^2/(AM)^2 puis que l'angle AMC est maximum quand AM^2 est minimum -> ok
3.En se plaçant dans le plan (ABH), déterminer la position du point M qui minimise AM, puis calculer la valeur minimale de AM.

Pour le point 3, je vois bien que le point M est situé sur le pied de la hauteur du triangle ABH pour sommet A pour que AM soit minimal, est-ce que c'est cela qu'il faut démontrer ? Je ne vois pas comment faire, donc merci d'avance si vous avez une piste.
-----

[lper]

voici la figure.

[gg0]

Théorème de Pythagore.

Cordialement.

[lper]

Je ne cherche pas à calculer AM, je cherche à démontrer que la position du point M est telle que AM est perpendiculaire à BH selon ce qui est demandé : "déterminer la position du point M qui minimise AM".

[A voir en vidéo sur Futura]

[gg0]

Justement,

le théorème de Pythagore permet de le prouver. C'est bien à ça que je répondais.

[lper]

Ok, je suppose qu'il faut donc développer selon le triangle ABH rectangle en A et trouver ainsi en fonction de M ?

[gg0]

AM²=AH²+HM²

Comment faire pour que AM (donc AM²) soit le plus petit possible ?

[lper]

Vous supposez que AHM est un triangle rectangle en H ?

[gg0]

Ah pardon,

j'ai oublié que H était un point du cube. Remplace H par H', où H' est " le pied de la hauteur du triangle ABH pour sommet A" comme tu le disais : AM²=AH'²+H'M²

[Médiat]

Bonjour cher lper (cela faisait longtemps )

Soit N un point quelconque de HB, alors le triangle AMN est rectangle en M, et par Pyhthagore AN² = AM² + MN² qui est minimum quand ...

[EDIT] Pas les mêmes notations, mais la même réponse que gg0

[lper]

Merci beaucoup, on va regarder apres manger. C'est tres gentil pour ta rapidité Mediat !😉

[lper]

Encore merci à vous deux d'avoir pris le temps de nous aider, c'était si, enfin...
Je vous tiendrai au courant car je me demande si l'exercice ne demandait pas plutôt une démonstration en utilisant les propriétés des vecteurs avec les produits scalaires en faisant par exemple intervenir l'angle et son cosinus.

[lper]

Juste pour vous donner des nouvelles, apparemment la démonstration était inutile, il suffisait de déterminer l'emplacement du point M, comme quoi l'énoncé d'un exercice peut devenir vite ambigüe.