Bonjour, voici un problème que je m'efforce de résoudre mais je n'ai aucune piste de comment le commencer, merci de l'attention :
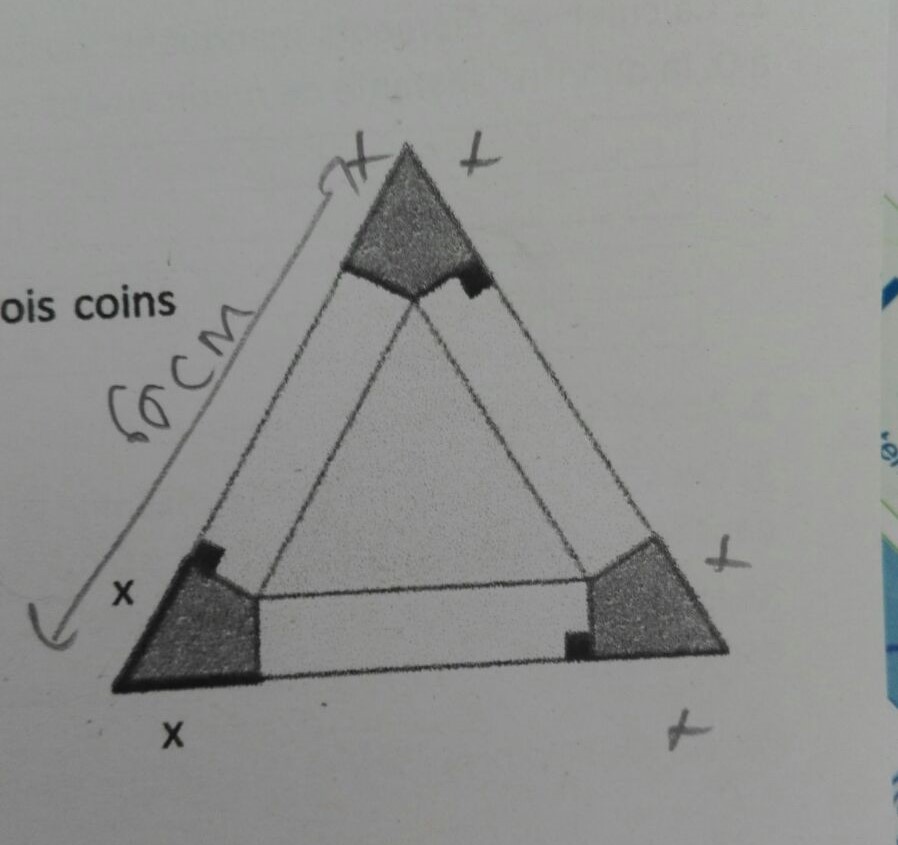
On découpe dans un triangle équilatéral de côté 60 cm, les trois coins grisés pour former une boîte triangulaire sans couvercle.
Déterminer la valeur de x pour laquelle le volume est maximal.
Une piste : exprime le volume en fonction de ce que tu connais (60) et en fonction de x.
On trouve des chercheurs qui cherchent ; on cherche des chercheurs qui trouvent !
J'ai essayé mais le volume c'est le produit de l'aire de la base et l'hauteur mais il me manque des info pour avoir l'hauteur de la boîte, merci
pas forcement hauteur*base.
moi, je n'arrive pas à construire un "cylindre" de base triangulaire si c'est ce à quoi tu penses, mais une pyramide.
essaye un petit découpage pour voir comment la construire....
ps : il faut plier chaque partie.
Bonsoir.La boîte a pour base un triangle équilatéral de côté .?. dont tu peux déterminer la hauteur pour en calculer l'aire.Envoyé par Angy98
La hauteur de la boîte, c'est tout simplement x une fois que tu as redressé les côtés rectangulaires. Les parties grisées sont retirées.
Duke.
EDIT : @ ansset : je ne comprends pas l'histoire des pyramides... Je vois plutôt un "prisme" triangulaire auquel on a retiré une des deux bases... non ?
Dernière modification par Duke Alchemist ; 30/08/2016 à 20h19.
pas de soucis, j'ai vu/lu l'exercice de façon bien compliqué.
à savoir construire une forme avec uniquement les zones grisées, pas l'inverse.
ce qui est plus complexe.
Bonsoir !
Comme je vois les choses, la hauteur de la boite augmente certes avec x, mais n'est pas x, sinon les parties grisées seraient des losanges et on aurait pas les angles droits qui sont marqués...
Combien y-a-t-il de façons différentes de voir cette boite ?
non, ce n'est pas x.
mais on connaît l'angle en chaque coin, donc le demi angle.....
encore désolé pour mon interprétation ubuesque de l'énoncé.
Bonsoir.
Bien relevé Kairn
En effet, la hauteur n'est pas x mais on peut la déterminer assez rapidement avec la bissectrice de l'angle au sommet du triangle dont on connait la valeur et un peu de trigonométrie dans un triangle rectangle.
Je ferais mieux de mieux regarder les schémas avant de faire des remarques
Cordialement,
Duke.
Bonjour,Bonsoir.
Bien relevé Kairn
En effet, la hauteur n'est pas x mais on peut la déterminer assez rapidement avec la bissectrice de l'angle au sommet du triangle dont on connait la valeur et un peu de trigonométrie dans un triangle rectangle.
Je ferais mieux de mieux regarder les schémas avant de faire des remarques
Cordialement,
Duke.
Une piste ou pas ?
Il faudrait ajouter des lettres au sommet des angles pour y voir plus clair!
La hauteur d'un triangle équilatéral est en même temps médiatrice, médiane etc... me trompé-je ?.
La hauteur partage le côté du triangle en deux parties égales
Le dessin laisse apparaître des rectangles (l'angle droit est noté et les côtés étant parallèles et égaux)
Pour trouver la surface de base:
Le côté du triangle intérieur, la base de la boîte est égal à 60-2x, la hauteur partage en 2 le côté, le demi-côté est égal à 30-x
Il faudrait peut-être utiliser le théorème de Pythagore ? triangle rectangle dont l'hypothénuse est le double d'un des côtés de l'angle droit. N'existe-t-il pas un théorème là dessus?
pour la hauteur de la boîte:
Si on prend la bissectrice de l'angle du grand triangle isocèle, elle partage en 2 angles de 30°, le petit triangle formé est un triangle rectangle dont le 3ème angle est de 60° et pareil , l'hypothénuse est égal à la moitié d'un côté donc de la hauteur de la boîte
Après chéplu surtout si je suis dans l'erreur
J'aurai essayé, mal probablement
Pernelle
Je suis la discussion. La réponse va finir par aboutir.
Je vois, j'oublie. Je fais, je retiens.
ben, la réponse est connue des intervenants maintenant ( enfin ceux qui ont fait le calcul )
c'est pas sorcier du tout.
mais c'est au primo posteur qu'il revient d'intervenir , mais qui n'est pas revenu.
erratum
J'ai écrit:
-
pour la hauteur de la boîte:
Si on prend la bissectrice de l'angle du grand triangle isocèle, elle partage en 2 angles de 30°, le petit triangle formé est un triangle rectangle dont le 3ème angle est de 60° et pareil , l'hypothénuse est égal à la moitié d'un côté donc de la hauteur de la boîte
-
C'est l'hypoténuse est égale au double d'un côté de l'angle droit
Pernelle
plus simple de dire que si h est la future hauteur de la boite:
tg(30°)=h/x
Je n'ai pas encore révisé la trigonométrie
Quant à la personne qui a posté à la mi-aou...ce devait être un devoir de vacances et,n'étant pas revenu, nous avions envie d'avoir la solution.
Qui rédige le tout clairement?
Pernelle
si tu veux.
donc j'écrivais ( trigo ) que tg(30°)=h/x soit
ici pour le demi-angle d'un sommet sa tangente =coté opposé/coté adjacent
donc h=xtg(30°)
par ailleurs la surface du triangle équilatéral ( surface de base de la boite ) = a²rac(3)/4 , si a est le coté de ce triangle.
cela se calcul aussi avec la trigo.
ici a=60-2x d'après les données.
de fait on a même pas besoin de calculer ses valeurs.
en effet.
la hauteur h est prop à x : h=kx
la surface base est prop à a² soit à (60-2x)²
donc le volume de la boite est prop à x(60-2x)²
soit un polynome de degré 3 en x.
dont la dérivée ( polynôme de degré 2 ) s'annule en deux points x=10 et x=30.
seul x=10 correspond à une solution "physique" qui correspond à un maximum ( l'autre annule la base de la boite et correspond à un minimum )
ps : en fait le dessin est très proche de l'optimum.
Mille mercis Annset,
Cela me dépasse, je ne me suis recyclée que jusqu'en 4ème et pas encore la trigo
Les dérivées sont du niveau lycée et j'ai oublié il y a belle lurette!
Ceci dit, il n'y a pas plus "simple", même si c'est plus long à rédiger?
Ma "piste" ne menait-elle pas à Rome?Où du moins ne parcourait-elle pas une portion du chemin? Je serais probablement arrivée dans une impasse ?
J'espère que tout cela va servir à quelques lecteurs intéressés !
Bonne rentrée à ceux qui sont en âge
Pernelle
tout ce que tu écris est juste.
et si tu prolonges tous tes calculs tu trouverais certainement ( avec un tout petit peu de trigo )
h=x/rac(3) et
S ( surface du petit triangle ) =(rac(3)/4)a² avec a=(60-2x)
d'où un volume total
V=x(60-2x)²/4 ( en cm^3 )
ensuite à défaut de savoir trouver un maximum avec les dérivées, on peut faire un tableur simple excel et/ou une courbe
pour voir les valeur de V pour x=0,2,4,6,8,10,12,14,........
Chic, cela me rassure et m'encourage à continuer mon recyclage!
Mille mercis Annset pour avoir pris le temps et la patience de répondre à mes questions
Pernelle
Bonjour,
Je sais que cela fait longtemps que j'ai posté disons que j'ai un peu laissé de côté l'exercice
Mais je veux quand même comprendre : je comprends le fait que h=x/rac(3) mais je ne vois pas comment en arriver à là : " S ( surface du petit triangle ) =(rac(3)/4)a² avec a=(60-2x) "
Pourquoi a^2 ? Et pourquoi rac(3) divisé sur 4 ?
c'est la formule de la surface d'un triangle équilatéral de coté a.
que l'on peut retrouver.
le demi angle d'un sommet vaut 30°
donc la hauteur du triangle est H=a*cos(30°)=a*rac(3)/2
la surface d'un triangle= base*hauteur/2
ici base=a donc
S=a*a*(rac(3)/2)/2=(rac(3)/4)a²
quand à a=60-2x , c'est juste la description de l'énoncé.
Merci pour ce problème sympa.
On le trouve aussi avec comme figure un carré et on obtient le même résultat: 1/6 du coté.
Je vois, j'oublie. Je fais, je retiens.
Maintenant je comprends mieux !
Merci d'avoir répondu
