Probleme de Math 1er S

[comando974]

Bonjour,

Mon prof ma donner un DM à faire pendant les vacance mais je ne sais pas comment mis prendre!
Il y a un rapport avec les fonction mais je ne vois pas le quels.

1) Pour réaliser un chenal d’évacuation des eaux à section rectangulaire de 4m de long, on dispose d'une bande en zinc de 32cm de large.
Comment choisir de plier cette bande de zinc afin que le chenal puisse accueillir un volume d'eau maximal ?

2) Un éditeur de livre recommande que chaque page d'un beau livre contienne 500cm² de texte imprimé et possède des marges inférieur et supérieur de 5cm et des marges gauche et droite de 4cm.
Déterminer les dimension d'une page entière afin que la consommation de papier soit minimale.

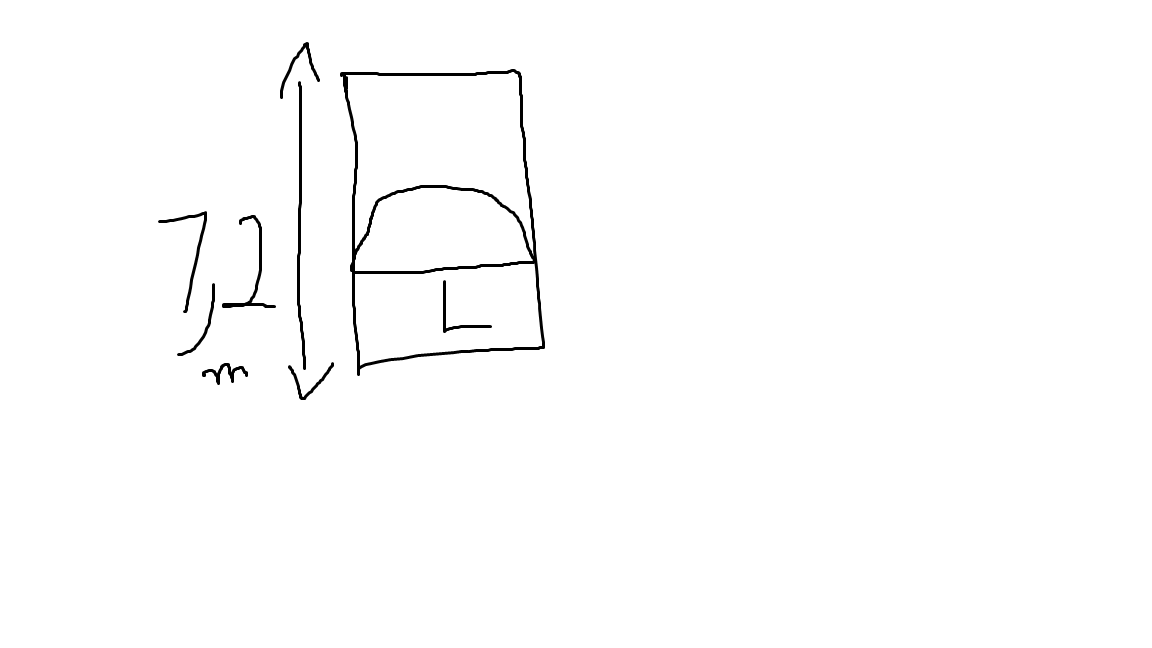
3) On perce dans la paroi d'une chambre mansardée une ouverture formée d'une vitre rectangulaire claire surmontée d'une vitre semi-circulaire colorée qui transmet quatre fois moins de lumière par unité d'aire que la vitre claire.
La hauteur totale l'ouverture mesure 1.20m et la largeur ne peut dépasser 2m.
Déterminer la largeur de l'ouverture qui laisse passer le plus de lumière. Arrondir au dixième.

J’espère que vous pourrait m'aider
Merci d'avance
-----

[gg0]

Bonjour.

effectivement, on peut t'aider. Lis ce fil : http://forums.futura-sciences.com/ma...ces-forum.html. Puis reviens en en ayant tenu compte.

Cordialement.

[Tpe de ssi]

J'aimerais bien m'entrainer en faisant l'exercice mais il manque des données non ? Ou les problemes sont ils resolvables tels quels? Sinon je cherche et je vous présente mes résultats
Merci d'avance

[ansset]

bsr,
toutes les données sont là pour chaque exercice.
commence par le premier et dis nous ce que trouve ou bien ce qui bloque.
ps : à part, " je n'y comprend rien" stp !
Cordialement.

[A voir en vidéo sur Futura]

[Tpe de ssi]

En fait il faut savoir en combien plier afin d'obtenir le volume le plus grand possible
On sait que V=L*l*H (j'imagine qu'on le plie de sorte a faire un parallélépipède)
or L(le grand L c'est bien longueur ?)=4m=400cm
Et on sait que la hauteur depend de comment on plie, le pli est symétrique donc (lorsque on plie ce n'est pas fermé puisque c'est un chenal d'évacuation, J'ai du chercher sur internet pour comprendre x)
on appelle x la "taille" de la pliure
avec 0<2x<32 <=> 0<x<16
V=400*(32-2x)*x
<=>V=12800x-800x²

Donc On voit que a est négatif (-8) donc avec la formule -B/2a on a le sommet et donc le max donc S=8
Il faut plier de 8 cm de chaque coté de la largeur de la bande
Je sais pas très bien rédiger désolé
Est ce que mon raisonnement est juste ?

[gg0]

Bonjour.

Ton x est bien H ? dans ce cas, je suis d'accord.
Attention à la multiplication des lettres pour le même nombre, H, x, S !!!

Cordialement.

[Tpe de ssi]

En effet j'ai bien pris H=x
Il etait mais la prochaine fois je ferais attention aux lettres. Je fais le prochain et je vous envoie ma reponse

[gg0]

"Il etait mais la prochaine fois ..."
En français, ça dit quoi ???

[Tpe de ssi]

Il était tard mais la prochaine fois je ferais attention. Ma pensée va plus vite que mes mots

[jacknicklaus]

1) Pour réaliser un chenal d’évacuation des eaux à section rectangulaire de 4m de long, on dispose d'une bande en zinc de 32cm de large.
Comment choisir de plier cette bande de zinc afin que le chenal puisse accueillir un volume d'eau maximal ?

Note : En enlevant la condition rectangulaire, on a un profil de "pliage" plus efficace : la gouttière en demi-cylindre.
la section est alors L²/2pi, qui est plus grande que la section rectangulaire optimale L²/8. Toujours avec une même largeur de zinc L.

[Espadon974]

Bonsoir ! Mon professeur de math m'a également donné cet exercice et je ne vois pas du tout comment l'aborder pourriez vous juste me donner la manière de le faire svp. J'ai essayer avec des équations mais le fait de devoir trouver un maximum me gêne. Pourriez vous m'aider svp.

[gg0]

Tu pourrais quand même lire ce qui précède !!!

[Espadon974]

J'ai lu ce qui précède et Tpe de si donne la réponse a un moment donné mais dans son message je ne comprends pas le dernier paragraphe. Il dit " a est négatif (-8) " mais d'où sort le -8 ?

[gg0]

Il fait référence à un cours que des trinômes du second degré, notés ax²+bx+c qui ont un maximum (si a<0) pour x=-b/(2a). en fait, c'est -800.
Mais on peut aussi noter que 12800x-800x²= -800(x-8)²+51200 (forme canonique)

Cordialement.

[Espadon974]

Ah d'accord merci pour votre aide !

[Espadon974]

Je suis actuellement en train de faire le dernier problème (du haut de cette page, le problème avec les vitres) et je bloque à un endroit.
Il faut dans ce problème trouver l'aire des vitres rectangulaire A2 et semi-circulaire A1 pour lesquelles une luminosité maximale passe. Donc j'ai écris cela:
lumière= A1/4+ A2 ; car A1 laisse passer 4 fois moins de lumières
A1= (Pi*r²)/2 ; r=rayon du demi-cercle= x/2 ; x désignant la largeur qui peut atteindre 2m maximum
A1= (Pi*(x/2)²)/2 = (Pi x²/4)/2 = (Pi x²)/8
A2= H*x ; H= hauteur du rectangle= 1.2-r = 1.2-(x/2) = (1.2*2-x)/2 = (2.4-x)/2
Donc: lumière = A1/4+A2 = ((Pi x²)/32)+((2.4-x)/2)(x) = ((Pi x²)/32)+((2.4x-x²)/2)
=((2Pi x²)+(2.4x-x²)32)/64 = ((2Pi x²)+76.8x-32x²)/64

Voila j'en suis à là pouvez vous me dire si mon résonnement est bon et si oui pouvez me dire comment continuer parce que je n'arrive pas à aller plus loin. Merci d'avance.

[jacknicklaus]

le calcul et le raisonnement sont bons. réarrange tes termes pour obtenir une forme plus simple du type x(1.2 - k.x) où k est un nombre positif que tu calculeras. puis utilise ton cours pour déterminer la valeur maximale d'un polynome du second degré sous une forme factorisée.

[Mordo]

En fait il faut savoir en combien plier afin d'obtenir le volume le plus grand possible
On sait que V=L*l*H (j'imagine qu'on le plie de sorte a faire un parallélépipède)
or L(le grand L c'est bien longueur ?)=4m=400cm
Et on sait que la hauteur depend de comment on plie, le pli est symétrique donc (lorsque on plie ce n'est pas fermé puisque c'est un chenal d'évacuation, J'ai du chercher sur internet pour comprendre x)
on appelle x la "taille" de la pliure
avec 0<2x<32 <=> 0<x<16
V=400*(32-2x)*x
<=>V=12800x-800x²

Donc On voit que a est négatif (-8) donc avec la formule -B/2a on a le sommet et donc le max donc S=8
Il faut plier de 8 cm de chaque coté de la largeur de la bande
Je sais pas très bien rédiger désolé
Est ce que mon raisonnement est juste ?

Bonjour, pouvez-vous être un peu plus explicite dans votre raisonnement car je me suis égaré au moment ou vous parliez d'utiliser la formule x= - b / 2a..

[Espadon974]

Jacknicklaus en ayant mon résultat ((2Pi x²)+76.8x-32x²)/64 est-ce que je peut directement essayer de calculer le maximum en calculant alpha: -b/2a ? Sachant que le resultat que je dois donner à la fin ne doit pas etre exact mais aproximatif.

[Espadon974]

Bonjour mordo, Tpe de ssi venait de trouver un trinome de second degré donc il a calculer le sommet de sa courbe avec la formule -b/2a pour trouver le maximum puisque a<0 donc la parabole est tourné vers le bas.

[Mordo]

Merci pour cette réponse @Espadon974 maintenant j'y vois plus claire!

[Mordo]

J'aimerai vous faire part de mon raisonnement concernant l'exercice 2) :

Tout d'abord, j'ai schématisé le problème par un grand rectangle représentant une page entière avec les notations suivantes: Aire 1 noté A1; Longueur 1 notée L1; largeur 1 notée l1.
Puis, un autre rectangle avec les notations: Aire 2 qui est égale à 500 cm² = L2 x l2.
Sachant que: chaque pages possèdent des marges inférieures et supérieures de 5 cm et des marges de gauches et de droites de 4 cm,
je peux conclure que L1 = L2 + 2 x 5 / l1 = l2 + 2 x 4 / A1 = A2 + 2 x ( 5 x l1 ) + 2 x (4 x L2 )
A1 = A2 + 10l1 + 8L2
J'exprime L2 en fonction de l1,
alors A2 = L2 x l2
=> 500 = L2 x l2

On sait que l2 égale l1 - 8 d’où L2 = 500 / l1 - 8 donc A1 = 500 + 10l1 + 8 x (500 / l1 - 8 )

A1 = 500 + 10l1 + 4000
l1 -8

A1 = 500l1 - 4000 + 10l1^2 + 4000
l1 - 8

A1 = 10l1^² + 420l1
l1 - 8

À stade j'ai nommé l1 => x

A1 = 10x^2 + 420x
x - 8


Et maintenant je suis quelque peu bloqué, pourrais-je avoir de l'aide?
Ou une explication qui pourrait m'être bénéfique pour la suite de mon exercice?

Je vous remercie d'avance, cordialement.

[jacknicklaus]

Jacknicklaus en ayant mon résultat ((2Pi x²)+76.8x-32x²)/64 est-ce que je peut directement essayer de calculer le maximum en calculant alpha: -b/2a ? Sachant que le resultat que je dois donner à la fin ne doit pas etre exact mais aproximatif.

bien sûr tu peux !

Commence par regrouper en un seul tes deux termes en x², pour obtenir ton "a", le facteur en x².
et que vois tu à tes yeux esbaudis ??
hein !??
un beau polynome sous une forme sympathique que tu connais bien, et lui appliquera ta formule magique -b/2a.

[Espadon974]

Ok merci donc je ne tient pas en compte le dénominateur 64 ? Parce que c'est cela qui me gênait en fait.

[jacknicklaus]

je vois pas où gêne le 64.

((2Pi x²)+76.8x-32x²)/64 = (2Pi/64) x² + (76.8/64) x - (32/64) x² = x²(*** - ***) + x 1,2 = a x² + b x

je te laisse compléter les *** dans (*** - ***), ce qui te donnes le "a". Que tu reporteras dans "-b/2a", et dont tu pourras alors faire le calcul approché comme demandé.

[Espadon974]

Ok donc en complétant les étoiles ça donnerait : x²((2Pi/64)-0.5)+1.2x ?
J'ai gardé 2Pi/64 au lieu de mettre le résultat approché pour avoir plus de précision.

[Tpe de ssi]

je peux conclure que L1 = L2 + 2 x 5 / l1 = l2 + 2 x 4 / A1 = A2 + 2 x ( 5 x l1 ) + 2 x (4 x L2 )

Je vois pas comment tu peux conclure ca :/
A1=(10+L2)(l2+8) mais c'est tout (enfin selon moi

Du coup comme on nous demande de conserver l'aire de 500 cm² je comprends pas comment on deduit les dimensions minimum, etant donné que lorsqu'on en augmente la largeur on diminue la longueur.
Merci de votre aide

[Tpe de ssi]

Je suis pas d'accord avec le raisonnement selon moi la vitre semi circulaire est en face de la vitre rectangle donc on a
Lumiere = Aire rectangle - aire semi circulaire + Aire semicirculaire/4

Avec aire semicirculaire = pi * (L/2)²/2
L/2 = rayon
divisé par 2 parce que c'est un demi cercle

(je sais pas dessiner x) mais ca illustre bien ce que je veux expliquer
Du coup on obtient a la fin
pour tout x appartient [0;2]
lumière=1,2L - pi*L²/2² + (pi*L²/4)/4
lumière= 1,2L - (pi*L²)/4 + pi*L²/16
lumiere = 1,2 L - 3/16*pi*L²
donc a l'aide de -b/2a puis que a est négatif le sommet correspond au maximum on voit que L pour que la lumière soit max est de 192/(60*pi)

[Tpe de ssi]

Toujours la meme question

[Chirurgien 17]

Bonjour !
J'ai exactement le même énoncé de maths (je suis en première Semaine) et je ne comprends pas d'où vient le (32-2x) si quelqu'un pourrait me donner plus d'information. J'ai quand même suivit la formule avec le (32-2x) et j'ai fais delta même si ça m'a pas servir à grand chose puis je suis partie pour calculer alpha et beta. Le alpha me donne 8 mais le beta me donne 0 ?? Du coup ça veut dire quoi ? Que si je plie 8 cm ça me donne le volume max ?