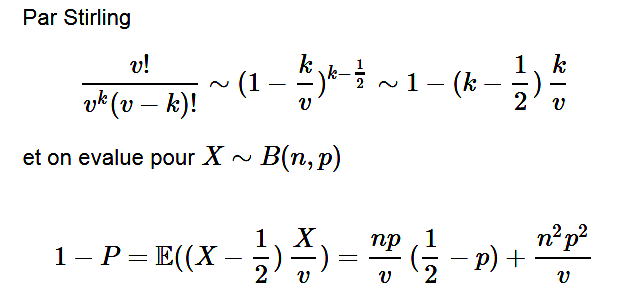Calcule de proba : 2 parmi n et plusieurs tirages avec remise

[AmigaOS]

Bonjour

J’avais vu la vidéo d’un théoricien du complot(en allemand) qui fait un calcul de probabilités pour nous prouver qu’il est TRES improbable qu’un journaliste assiste à 2 attentats différents. A la fin il conclut qu’on doit être frappé par 56.2 éclaires avant d’assister à deux attentats (lol). Le problème c’est qu’il fait une énorme erreur car il néglige la taille de l’échantillon. Dans son calcul il oublie d’inclure le nombre de journalistes qui existent en Europe. Ce qui change tout. Du coup je voulais lui répondre mais je me rends compte que je ne connais moi-même pas le bon calcul. Et j’ai eu du mal à trouver sur Google. A chaque fois il y a un détail qui est différent.

Du coup voila les donnés (bon on va considérer que c’est ça ) :
Probabilité d’être proche d’un attentat en Europe par an : 0.000054
Nombre de Journalistes en Europe : 320 000

Comme dit plus haut j’ai donc besoin d’aide pour calculer la probabilité qu’un journaliste européen assiste à 2 attentats en Europe la même année.

Merci
-----

[gg0]

Bonjour.

D'abord pourquoi vouloir répondre à ce genre de vidéo ?
Ensuite, ces questions ne sont pas des questions de probabilité, les attentats ne sont pas une épreuve aléatoire, sans parler de la notion de "proche d'un attentat". tellement floue !

Mais pour ton problème de probas pures, je note a la probabilité qu'un événement arrive à un individu dans l'année, et je suppose que ces arrivées sont indépendantes (donc ça peut arriver avec la proba a à celui à qui c'est arrivé 20 fois (*). La probabilité qu'il en arrive au moins 2 est la proba contraire à l'arrivée 0 ou 1 fois. Cette proba dépend évidemment du nombre d'attentats, je vais le noter N. Donc a est la probabilité d'être proche d'un attentat donné parmi les N (**) La loi binomiale peut être utilisée, et donne P(0)+P(1)=(1-a)^N+Na(1-a)^(N-1), et donc la proba d'être proche de 2 attentats est, pour chaque personne, 1-((1-a)^N+Na(1-a)^(N-1)) = b.

Ensuite, comme il y a 320000 journalistes, en les supposant parfaitement équirépartis (ce qui est grossièrement faux), la probabilité qu'au moins un journaliste ait été présent lors de 2 attentats est la probabilité contraire de "aucun n'a été présent plus d'une fois", donc est 1-(1-b)^320000.

Finalement, avec ces hypothèses assez fantaisistes on obtient un calcul qui n'a pas trop de sens, mais qu'on peut essayer de faire. Pour b=0.0000001, on trouve environ 3%; en partant de a=0.000054 (d'où peut bien sortir cette valeur ??? il y a eu 50 000 personnes au stade de France, plusieurs milliers à Nice et Berlin, même en réduisant à 0 au stade de France, on est au moins à 3000, sur 300 millions d'européens, ce qui fait 1/100000=0.00001, c'est le double !!), et en prenant N=5, on obtient 0,000096.
Qu'en déduire ? Rien !! Je l'ai dit du début, il ne s'agit pas d'une situation probabiliste.
Et même dans des situations probabilistes ... La probabilité que quelqu'un gagne au loto 2 fois est très faible, même en tenant compte du nombre de joueurs est faible. Pourtant c'est arrivé.

Donc si tu veux vraiment attaquer cette vidéo, c'est plus sur l'aspect "faux" de l'usage des probas que sur des calculs fantaisistes qu'il faudra t'appuyer. La donnée "Probabilité d’être proche d’un attentat en Europe par an : 0.000054" n'a pas de cohérence !!! Ce qui s'est passé en 2015 n'avait rien à voir avec 2014, ni avec 2016. Faire des calculs pour "prouver" que quelque chose ne s'est pas passé n'est qu'un habillage pseudo-scientifique de la phrase "je n'y crois pas".
Une grande part des arguments des négationnistes est basée sur ce genre de considération idiote : Les coïncidences arrivent, dire "c'est peu probable" est idiot !! C'est justement parce que c'est peu probable qu'on parle de coïncidence

Cordialement.


(*) on se rend compte que cette modélisation est incorrecte, la possibilité dépend aussi du temps qui reste dans l'année, si c'est arrivé 20 fois, l'année est presque finie, la proba n'est plus a.
(**) en introduisant N, on élimine la critique de (*), mais a a changé de signification, et de plus c'est une valeur variable, il y avait bien plus de gens au stade de France que dans l'église où le curé a été tué.

[AmigaOS]

D'abord pourquoi vouloir répondre à ce genre de vidéo ?

Parce que ça m’amuse tout simplement. ^^ Et parce que j'avais envie de voir ce que donne le vrais calcul.

Ensuite, ces questions ne sont pas des questions de probabilité, les attentats ne sont pas une épreuve aléatoire, sans parler de la notion de "proche d'un attentat". tellement floue !

Je sais que tous ça est complètement flou, que ça dépend de tellement d’autres facteurs et que le résultat sera précis à plus ou moins 99%, mais c’est juste pour corriger ses erreurs de calculs et montrer (si on veut exprimer ça sous forme de probabilités) que même en prenant ses chiffres foireux, c’est pas aussi improbable que ce qu’il trouve lui.

(donc ça peut arriver avec la proba a à celui à qui c'est arrivé 20 fois (*).

Oui, ce qui est déjà arrivé à un individu n’influence pas la proba de ce qui peut encore lui arriver. (Si on considère qu’il ne change pas sa vie...)

La probabilité qu'il en arrive au moins 2 est la proba contraire à l'arrivée 0 ou 1 fois.

Je ne comprends pas cette phrase. :/ Que veut dire "l'arrivée 0 ou 1" ? Le fait que ça arrive 0 fois ou une fois ? Et la probabilité inverse c’est genre : 97% est l’inverse de 3% ?

Cette proba dépend évidemment du nombre d'attentats, je vais le noter N.

Oui c’est mieux

en partant de a=0.000054 (d'où peut bien sortir cette valeur ???

Enfaite il prend sur Wikipedia la probabilité d’être victime d’un attentat en Europe en un an et la multiplie grossièrement pas 1000 pour avoir "environ" celle d’y assister. (Mais il garde quand même 5 chiffres significatifs dans sa vidéo) xD

La probabilité que quelqu'un gagne au loto 2 fois est très faible, même en tenant compte du nombre de joueurs est faible. Pourtant c'est arrivé.

C’était mon argument ça ^^ (enfin, je l’ai moi-même vu ailleurs)

[gg0]

"Oui, ce qui est déjà arrivé à un individu n’influence pas la proba de ce qui peut encore lui arriver. (Si on considère qu’il ne change pas sa vie...)"
Faux. Déjà, celui qui vient de mourir a peu de chances de mourir encore. Ensuite, a est une probabilité sur une durée limitée, qui n'a de sens qu'avant cette durée et est rarement une situation d'indépendance des réalisations.

"Je ne comprends pas cette phrase." finalement, tu la décodes bien.

Cordialement.

[A voir en vidéo sur Futura]

[AmigaOS]

Je vais préciser un truc en plus: Enfaite c'est non seulement parce que ça m’amuse de lui répondre mais aussi parce que j'avais prévu faire un article (ou vidéo, je verrai) dans le but d'expliquer l'erreur de la "négligence de la taille de l'échantillon".
Du coup après avoir réfléchis un bon bout de temps pour comprendre la nouvelle modélisation avec N, je me demande si je peux pas garder l'ancienne modélisation (qui est moins proche de la réalité).
Enfaite j'essaie de voir la chose de la manière la plus proche possible de la sienne pour ne pas devoir expliquer un truc complètement nouveau et trop loin de son truc.
Bien sûr je préciserai que la modélisation est foireuse et pourquoi...

Du coup faudrait considérer le problème de la manière suivante :
(Je fais une analogie avec des billes parce que j'ai du mal à me représenter dans ma tête la situation avec les attentats)
On a un sac remplit de 500 000 000 billes, tous de couleur bleu à l'exception de 320 000 qui sont vertes. Dans un an on en prends 27000 (=0.000054*500M) une par une pour les peindre en rouge et en les remettants à chaque fois. Quelle est la probabilité d'avoir peint une même bille verte 2 fois en rouge ? (pas forcement qu'une seule, mais juste le fait que ça arrive, je ne sais pas si ça change quelque chose au problème..)

Enfaite ce qui change par rapport la meilleure modélisation, c'est qu'au lieu de peindre N fois une certaine quantité de billes en rouge on le fait de manière progressive. N = nombre de fois qu'on peint une bille en rouge.

[gg0]

Je ne suis pas très à l'aise avec ce genre de calcul, d'autres auront peut-être une idée. Tu peux éventuellement faire un programme de simulation, à faire tourner un grand nombre de fois.

[AmigaOS]

Tu peux éventuellement faire un programme de simulation, à faire tourner un grand nombre de fois.

J'avais pensé à ça mais plutôt pour vérifier le résultat du calcul analytique.

J'ai posé ma question sur un autre forum en mettant directement le problème des billes et on 'a donné une énorme formule que je vais tenter de comprendre.

Par contre je me demande autre chose. Imaginons on a la probabilité d'être frappé par une éclaire dans un an (0.000000166) (c'est ce à quoi il compare tout à la fin de son calcul). Est-ce que pour calculer la probabilité d'être frappé n fois en un an par l'éclaire on peut faire 0.000000166^n ?

[gg0]

Non !

Cette "probabilité" n'a aucun sens, encore une fois, confondre une fréquence réelle (l'est-elle ?) avec une probabilité n'a pas de sens si on n'a pas une épreuve probabiliste.
Tu t'es fait manipuler par un trafiquant de calculs.

D'ailleurs, une grande partie de ceux qui ont été frappés une fois par la foudre ne le seront plus jamais : La foudre ne frappe pas les cercueils enterrés
Et inversement, certains alpinistes ont été frappés 2 fois par la foudre, mais ils sont dans des conditions favorisantes.


Par contre, dans une épreuve qu'on peut répéter indépendamment avec la même probabilité de réussite p, la probabilité d'avoir 2 réussites sur 2 épreuves est p². Mais rien à voir avec ton cas (c'est la même épreuve). Ton théoricien du complot est très faible en théorie !!!

[AmigaOS]

D'ailleurs, une grande partie de ceux qui ont été frappés une fois par la foudre ne le seront plus jamais : La foudre ne frappe pas les cercueils enterrés
Et inversement, certains alpinistes ont été frappés 2 fois par la foudre, mais ils sont dans des conditions favorisantes.

Oui ça dépends de là où on se trouve et du nombre de gens qui y survivent et tout. Mais pour son calcul il utilise la probabilité de la foudre pour la comparer à une autre. C'est juste théorique, il considère que c'est possible.

Non !
Cette "probabilité" n'a aucun sens, encore une fois, confondre une fréquence réelle (l'est-elle ?) avec une probabilité n'a pas de sens si on n'a pas une épreuve probabiliste.

Du coup si on considère qu'on ne meurt pas à cause de la foudre et que tous les gens sont répartis de manière parfaitement homogène sur le territoire et que la foudre a autant de chances de frapper partout à tout moment (et que les donnés sont correctes), est-ce que le calcul de P^n a du sens ? Si non, quel serrait le bon calcul ? Je ne connais pas bien la différence entre probabilité et fréquence..

Ton théoricien du complot est très faible en théorie !!!

Oui, comme moi
Mais lui il a carrément fait une division pour comparer. Il a trouvé que la probabilité d'être frappé par la foudre était 56.2 fois plus faible que d'assister à deux attentats, donc il en conclut qu'il faut avoir été frappé 56.2 fois par la foudre avant d'assister à deux attentats. x)

[gg0]

"Du coup si on considère qu'..." Non , le calcul qui donne p^n est relatif à une autre expérience.

"Oui, comme moi" . Alors pourquoi veux-tu traiter le problème ainsi ?

On peut toujours faire des calculs fantaisistes, mais si tu les fais, tu te conduis comme lui, alors que justement, ce qui est grave c'est de faire des calculs fantaisistes pour trafiquer la réalité. On ne dévalorise pas des calculs fantaisistes en en faisant d'autres, un peu moins fantaisistes.
La notion de probabilité d'une coïncidence est une absurdité : la coïncidence est un fait, pas une régularité probabiliste. Tu perds ton temps ...

[AmigaOS]

"Oui, comme moi" . Alors pourquoi veux-tu traiter le problème ainsi ?

Pour "Oui, comme moi", c'était juste pour dire que je suis pas très fort en proba (pour les calculs). C'est pour ça que je pose des questions ici.
Enfaite je veux montrer ce qu'il faut améliorer par rapport à son calcul (taille de l'échantillon...) et ensuite donner peut être un calcul qui a plus de sens en disant que même là on a négligé pleins de choses qui changent tout. Et ensuite expliquer ça :

La notion de probabilité d'une coïncidence est une absurdité : la coïncidence est un fait, pas une régularité probabiliste.

Ce qui annule l’intérêt des calculs précédemment corrigés...

[gg0]

Autrement dit, quand quelqu'un fait n'importe quoi, tu commences par faire comme lui, avant de dire que ça n'est pas ce qu'il faut faire !!!!

Bon, je ne vois pas l'intérêt de continuer. Désolé.

[AmigaOS]

C'est plutôt : quand quelqu'un fait n'importe quoi, je commence par expliquer comment il aurait fallut faire si sa méthode aurait eu du sens, avant d'expliquer ce qu'il aurait vraiment fallut faire.

[invitecf8b6a85]

Bonjour amigo
J'ai saisi ta question et ta volonté de comprendre si on peut ou non multiplier les probabilités. Je viens de moi mème être confronté aux mêmes questions et je pense l'avoir résolu en prenant pour modèle le dé de 6.
La réponse est non, on ne peut pas multiplier les probabilité.
dans ton exemple de foudre (plus simple que les attentats) il faudrait connaitre n le nombre de personnes du groupe et o le nombre de fois ou la foudre est tombée sur quelqu'un de ce groupe.
Si je ne me trompe pas, la probabilité d’être touché r fois (2 dans ton exemple) par la foudre = 1-((n-o)/n)exp r)

[invitecf8b6a85]

Erratum ! ca ne colle pas, je vais plancher sur le sujet

[AmigaOS]

Ah merci. J'attends alors

ta volonté de comprendre si on peut ou non multiplier les probabilités.

C'est bien ça Si ça ne marche vraiment pas alors je le ferrais pas..
n = 82 000 000
o = 14


Pour la formule du problème avec les billes on m'a proposé ça sur l'autre forum :

Avec :
b = 499 680 000
v = 320 000
n = 27000
p = v/(v+p)
k : le nombre de billes vertes obtenues en n tirages.