Périmètre d'une ellipse

[inviteb38b7130]

Bonjour, je voudrais savoir s'il existait à ce jour une formule exacte pour calculer le périmètre d'une ellipse.
-----

[gg0]

Bonjour.

Tout dépend de ce que tu appelles "exacte". La formule exacte pour le cercle est Pi D, où pi est justement le nombre par lequel on multiplie D pour obtenir le périmètre. Ce qui est exact, c'est que c'est le même pour tous les cercles, qu'il sert aussi pour calculer l'aire, et qu'on sait en obtenir des valeurs approchées décimales avec des milliards de décimales. Mais P=Pi.D n'est pas une formule exacte si tu fait du calcul décimal.
Pour l'ellipse, de la même façon, on a des formules avec les "fonctions elliptiques", qui donnent une "formule exacte" (avec égal), et on sait calculer les valeurs avec toute la précision voulue.

Cordialement.

[Dlzlogic]

Bonjour,
A ma connaissance, on ne connait pas de formule exacte pour la circonférence de l'ellipse. J'avais fait des recherches sur ce point il y a quelques années, et les résultats étaient unanimes : on ne savait pas le faire.
*** Hors sujet ***

[fartassette]

Bonjour,

Bonjour.

Mais P=Pi.D n'est pas une formule exacte si tu fait du calcul décimal.
Pour l'ellipse, de la même façon, on a des formules avec les "fonctions elliptiques", qui donnent une "formule exacte" (avec égal), et on sait calculer les valeurs avec toute la précision voulue.
Cordialement.

Entièrement d'accord avec ggo , ce n'est pas exacte si tu fait du calcul décimal .


le périmètre de l’ellipse a été déduis d'un calcul d'intégral si mes souvenirs sont bon




sont les axes de ton ellipse


Maintenant on remarque que si on pose

, on revient au périmètre d'un cercle

[A voir en vidéo sur Futura]

[invite8a1b1525]

Bonjour

le périmètre de l’ellipse a été déduis d'un calcul d'intégral si mes souvenirs sont bon

en effet, on peut calculer la longueur des courbes paramétrées "gentilles" avec une intégrale curviligne, la formule est assez simple. Pour une ellipse de demi-axes de longueurs a et b, le périmètre de l'ellipse est , ou encore

[inviteb38b7130]

Ce que je veux dire par "exacte" c'est seulement que quelque soit a et b les demi grand et petit axes, la formule reste la même.
Je cherche juste à savoir, s'il existe une formule (avec ou sans intégrale) qui permet de calculer de façon exacte le périmètre d'une ellipse.
Pas de valeurs approché

[Médiat]

Bonsoir,

Donc le message #5 répond pleinement à la question (c'est le cas particulier du calcul de l'abscisse curviligne d'une fonction paramétrée

[inviteb38b7130]

D'accord, mais, est-ce qu'il est possible d'obtenir une formule tout aussi exacte qui ne me fait pas utiliser de fonctions paramétrées ?

[invite8a1b1525]

D'accord, mais, est-ce qu'il est possible d'obtenir une formule tout aussi exacte qui ne me fait pas utiliser de fonctions paramétrées ?

heu..?? votre ellipse possède bien deux axes ? bon ben alors, vous connaissez les paramètres a et b.
Où le problème ?

[inviteb38b7130]

Parce que moi j'ai trouvé une formule qui me semble très convaincante et qui ne fait intervenir aucune fonction paramétrée ni même des sinus et de cosinus, la voici. Je vous conseil de tester avec GéoGebra, je l'ai déduite seul, et personnellement elle est plutôt au poil.

Cette formule fonctionne pour a>b quelque soit les valeurs de a et de b, l'approximation de GéoGebra me donne bien la même approximation que mes calculs. Si vous voulez, j'ai rédigé une fiche dans laquelle j'explique comment j'ai fait.
https://docs.google.com/document/d/1...nYY92YOlA/edit

[invite8a1b1525]

Bonjour, je voudrais savoir s'il existait à ce jour une formule exacte pour calculer le périmètre d'une ellipse.

oui, et vous le savez bien

[Médiat]

Parce que moi j'ai trouvé une formule qui me semble très convaincante et qui ne fait intervenir aucune fonction paramétrée

Ben si, c'est juste le cas particulier ou x = t et y = f(t)

[inviteb38b7130]

Cette formule était donc connue. Mais pourquoi ne l'écrit-on pas de la façon dont je l'ai présenté ?

[inviteb38b7130]

Au passage, quelqu'un peut-il me dire ce que signifie le E dans cette équation ?

[inviteb38b7130]

Ben si, c'est juste le cas particulier ou x = t et y = f(t)

Mais f(x) = ?

[invite8a1b1525]

Cette formule était donc connue. Mais pourquoi ne l'écrit-on pas de la façon dont je l'ai présenté ?

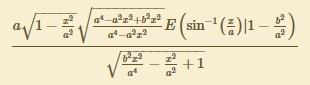
c'est la même intégrale que j'ai présentée, mais avec un changement de variable qui fait disparaître les fonctions trigonométriques, mais qui complique un peu la présentation (c'est subjectif, j'en conviens). Des changements de variables possibles, il y en a plein ! ...donc il y a plein de manières présenter un même résultat obtenu par une intégrale...

[Médiat]

Mais f(x) = ?

Regardez dans votre document !

[Dlzlogic]

Bonjour,
J'ai l'impression qu'il y a une ambiguïté dans l'expression "formule exacte".
Il existe des formules exactes pour calculer différentes choses (surfaces, volumes etc.).
Il existe d'autre part des définitions exactes, le périmètre de l'ellipse en est exemple : on sait écrire sa définition exacte, elle contient une intégrale, mais on ne sait pas trouver une formule exacte, simplement parce qu'on ne sait pas, au moins actuellement, trouver une primitive de la fonction considérée.
En d'autres termes, on sait calculer cette intégrale de la façon aussi précise que l'on veut, mais ce ne sera jamais qu'un résultat numérique approché.
Concernant l'ellipse, je crois me souvenir avoir vu une "formule approchée", c'est à dire une formule sans intégrale, qui permet d'obtenir une valeur de la quantité cherchée.

[invite0b618583]

En d'autres termes, on sait calculer cette intégrale de la façon aussi précise que l'on veut, mais ce ne sera jamais qu'un résultat numérique approché.

Comme l'a pointé gg0 au tout début : c'est la même chose pour le cercle. Le périmètre d'un cercle de diamètre 1 est pi. Nombre dont on ne pourras jamais avoir qu'une valeur numérique approchée. De la même manière on peut donner les formules exactex du périmètre d'une ellipse en utlisant des fonctions spéciales dont on peut calculer la valeur numérique avec une précision arbitraire.

[Dlzlogic]

Je pense que pour que Kiwi comprenne de quoi on parle, il faudrait préciser la différence entre une formule "exacte" et une formule qui ne l'est pas.
A moins que l'on fasse un amalgame entre "formule" et "résultat".

[invite8a1b1525]

mais on ne sait pas trouver une formule exacte, simplement parce qu'on ne sait pas, au moins actuellement, trouver une primitive de la fonction considérée.

Bien sûr qu' on sait "trouver" (disons "définir") les primitives des formules données ci-dessus. Mais le problème pour certains utilisateurs : elles ne s'expriment pas avec les 4 opérations usuelles. Mais ces personnes confondent le mot "exact" avec le fait de s'écrire uniquement avec les 4 opérations usuelles, comme si les fonctions exponentielle, cosinus, etc. n'étaient pas exactes...

[invite0b618583]

La formule est tout aussi exacte que celle avec pi. Ou d'une avec sinus ou cosinus.