Direction d'une fonction

[Matlabo]

Salut,
On a une fonction sous R
f(x) = x^2 + 6x - 16
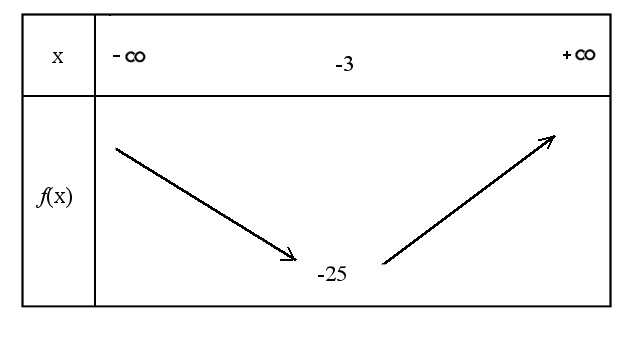
On sait que sous [-3 ; + l'infini ] la fonction est en augmentation

Alors on nous a demandé de chercher sa direction (si elle est en diminution ou en augmentation ) sous [ - l'infini ; -3 ]

Alors j'ai pris 3 et un nombre sous [ - l'infini ; -3 ] par ex -5
On appliquant la loi qui dit que si une fonction est en diminution alors

Si x1 < x2 alors f(x1) > f(x2)

Alors j'ai trouvé qu'elle était en dimunation

Je me demande si il suffit de prendre une valeur à peu près pour trouver sa direction

Et aussi je me demande comment dessiner le tableau de changement de direction d'une fonction contenant moins l'infini ou plus l'infini je me demande si on doit prendre une valeur à peu près....


Merci beaucoup😁
-----

[Matlabo]

x1 = -5
x2 = -3

f(-5) = -21
f(-3) = -25

Merci pour les réponses

[invitedd63ac7a]

En France on parle de fonction croissante (augmentation) ou décroissante (diminution). De toute façon il est insuffisant, pour connaitre le sens de variation d'une fonction, d'essayer sur deux valeurs particulières :

La définition dit
si pour tout x1 et x2 de l'intervalle I tels que x1<x2 on a f(x1)>f(x2) alors f est strictement décroissante sur I.

Il faut donc partir de x1<x2 deux réels de ]-Infini; -3] et montrer que f(x1)>f(x2).

Pour faire cela tu considères x1<x2 dans l'intervalle ]-Infini; -3]
et tu étudies le signe de f(x1)-f(x2).

[Matlabo]

Ok merci pour ta réponse j'ai compris .
Mais le probleme c'est quand nous a demandé de trouver l' Extrema de fonction f
Et aussi de dessiner un tableau de changement de direction de la fonction.
On sait que sur l'intervalle [-3 ; + l'infini [ elle est en croissance alors que sur l'intervalle [- l'infini -3 [elle est en décroissance

Merci pour l'aide ....

[A voir en vidéo sur Futura]

[Matlabo]

Moi ce qui me dérange c'est la présence de l'infink dans l'intervalle

[Matlabo]

......infini pas infink ( faute de frappe......)

[Matlabo]

Salut
Enfaite je cherche l'éxtrémum locale pas globale
Merci!!

[fartassette]

bonsoir,

tu sais dériver une fonction?

Si est un extremum local de ƒ, alors.Tu dois trouver le réel qui annule la dérivée.


autre possibilité: as tu appris a chercher les coordonnées du sommet d'une parabole?

[Matlabo]

Salut
merci pour ta réponse mais j'ai pas compris le dérivé

Ee dsl mais on a pas encore appris a chercher les coordonnées du sommet d'une parabole?
Merci

[invitedd63ac7a]

Le tableau de variation de f:

[Matlabo]

Ok
Mais là l'éxtrémum local le plus petit alors c'est -25 ??!
Et le plus grand??

Et puis - l'infini est plus petit que - 25 alors la fleche devrait monter de - l'infini à - 25
Merci

[fartassette]

Bonjour,


le tableau de variation indique que la fonction atteint son minimum en .C'est le seul extremum local

[Matlabo]

Ok merci beaucoup
Mais
- l'infini est plus petit que - 25 alors la fleche devrait monter de - l'infini à - 25
Merci

[invitedd63ac7a]

Ne confonds pas les valeurs des antécédents, les "x", et les valeurs des images de la fonction les "f(x)".
Quand x augmente de -infini à -3, les valeurs de f, les "f(x)", décroissent (diminuent) jusqu'en -25.
Quand x augmente de -3 à +infini, les valeurs de la fonction f , les "f(x)", croissent à partir de -25.
Ainsi, le -infini de la première ligne ne peut être comparé au -25 de la seconde.

Dans un tableau de variation on ne peut comparer que des nombres de même genre soient des antécédents entre eux, la première ligne, soit des images entre elles, la deuxième ligne.

[Matlabo]

Nnn dsl c'est une bétise����
Enfin je crois ....
Dites le moi ci c'est le cas
Merci

[Matlabo]

Encore une fois dsl j'ai pas vu le message
Merci pour la réponse