Point d'inflexion fontion polynome degré 4

[NickiNickiNicki]

Bonjour

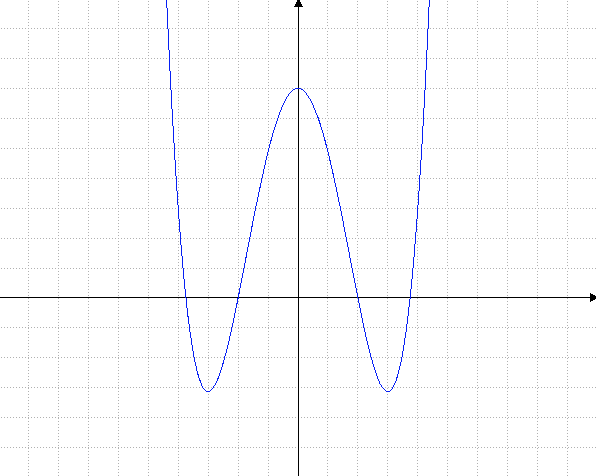
Je suis entrain de faire l'étude d'une fonction polynome f(x) = 1/8 (x² - 15)(x² - 4)

Je dois calculer les points d'inflexion de cette fonction, je n'ai pas de problème avec le calcul des points d'inflexion en soit, je sais qu'il faut calculer la dérivée seconde, dresser un tableau de signe et regarder si il y a un changement de signe là ou la fonction s'annulle. Mais si je développe la fonction avant de la dériver, elle sera ainsi un polynome de degré 4, et que je calcule la dérivée seconde de cette forme, j'obtient deux points qui se trouvent pas sur ma fonction... dois-je calculer la dérivée seconde de la fonction avec les paranthèses ? Mais je ne vois pas comment faire...

Merci d'avance de me lire, si quelqu'un à une idée...
-----

[jacknicklaus]

si je développe la fonction avant de la dériver, elle sera ainsi un polynome de degré 4, et que je calcule la dérivée seconde de cette forme, j'obtient deux points qui se trouvent pas sur ma fonction...

"j'obtient deux points qui se trouvent pas sur ma fonction" : je ne comprends pas cette phrase; peux tu mettre ici les calculs qui amènent cette conclusion?

[NickiNickiNicki]

f(x) = 1/8 (x² - 14)(x² - 4) (oops, c'est 14 et pas 15)
f(x) = 1/8 (x⁴ - 18x² + 56)
f(x) = 1/8x⁴ - (1 · 18)/8x² + (56 · 1)/8
f(x) = x⁴ - 18x² + 56
f'(x) = 4x³ - 36x
f''(x) = 12x² - 36

∆'' = 0² - 4 · 12 · (-36) = 1'728

x₁ = (-0-√∆) / 24 = 1,732
x₂ = (-0+√∆) / 24 = -1,732

Si je dresse un tableau de signe avec les valeurs ou x s'annul :

xkkkkkk–∞kkkkkkkkkk–1,732kkkkkkkkkk1,732kkkkkkkkkk+∞
f''(x)kkkkkkkkkk+kkkkkkk0kkkkkkk–kkkkkkk0kkkkkkk+

12(+/–1,732)² - 36 = 0
12(–2)² - 36 = 12
12(1)² - 36 = -24
12(2)² - 36 = 12

[jacknicklaus]

f(x) = 1/8x⁴ - (1 · 18)/8x² + (56 · 1)/8
f(x) = x⁴ - 18x² + 56

commencer par repérer l'erreur entre ces deux lignes.

[A voir en vidéo sur Futura]

[jacknicklaus]

12(+/–1,732)² - 36 = 0
12(–2)² - 36 = 12

je ne vois pas l'intérêt de ce calcul ? Tu en conclus quoi ?

D'autre part, en maths, on ne simplifie pas par 1.732. On garde tout le temps

[jacknicklaus]

f''(x) = 12x² - 36

tu ne peux pas simplement écrire
donc racines =

?

[NickiNickiNicki]

f(x) = 1/8x^4 - 9/4x^2 + 7
f'(x) = 1/4x^3 - 9/2x
f''(x) = 3/4x^2 - 9/2

∆'' = 0^2 - 4(3/4)(-9/2) = 13,5

x1 = -√∆ / 2a = -2,45
x2 = √∆ / 2a = 2,45

[NickiNickiNicki]

Oui je sais pas pourquoi j'ai mis ce 1,732 :/

[jacknicklaus]

f(x) = 1/8x^4 - 9/4x^2 + 7
f'(x) = 1/4x^3 - 9/2x

non. erreur de calcul.


et, pour la seconde fois (message #6) ne déroule pas la méthode du Delta pour un polynome sous la forme ultra-triviale x² - c = 0 !!!

[NickiNickiNicki]

D'accord, merci.. mais quand j'ai 1/8(x⁴ - 19x² + 60)

est-ce que ca donne : 1/8x⁴ - 19/8x² + 60/8, je peux faire multiplier par 8 ? ou c'est une grosse erreur d'algèbre, parce que j'ai fais comme ceci pour l'autre question de l'exerice, j'avais un graphe et 3 fonctions, je devais choisir parmi les 3, en dressant un tableau de signe et de variation pour chacune, et je trouve les minimums et le maximum correct mais mnt je ne sais pas si j'ai développer juste ou non..

Je me suis un peu embrouillée la tête ;/

[NickiNickiNicki]

Voila, j'ai remis de l'ordre, donc on a 12(x - 3) donc deux racines +/- √3

Mais je ne comprends pas quoi faire avec maintenant. Si je dresse un tableau de signe :

xkkkkkkkkkk-√3kkkkkkkkkkk√3
f''(x)kkk-kkkkk0kkkkkk-kkkkk0kkkkkkk+

Du coup il n'y a pas de changement de signe... donc -√3 n'est pas un point d'inflexion.. mais la fonction est symétrique.. je sais pas pourquoi je bug sur cet exercice

[Lil00]

Il y un problème dans ton tableau de signes : 12(x²-3), et non 12(x-3) comme tu l'écris, est-elle positive ou négative pour x<racine(3) ?

[jacknicklaus]

Je me suis un peu embrouillée la tête ;/

c'est très simple. Si , tu as le droit d'écrire


tu peux en déduire

tu dois conserver le 1/8

mais si tu écris : je cherche à résoudre f"(x) = 0 tu as le droit de tout multiplier par 8. Comme 8 x 0 = 0 ca donne :
mais tu n'as pas le droit de dire que cette expression est f"(x) car f"(x) et 8f"(x) c'est pas pareil.

De même pour poursuivre, tu as le droit de tout diviser par 12, parceque 0/12 = 0 et donc tu peux écrire

[NickiNickiNicki]

Merci pour ton aide, donc je peux étudier les variations de la fonction avec x⁴ - 18x² + 56 ?
J'ai utilisé l'expression avec 1/8 pour calculer les extremas, après avoir trouver les 0

Et pour calculer les points d'inflexions, j'ai donc +/- √3, oui je me suis trompée, il y a un changement de signe donc j'ai deux points d'inflexion de coordonnées (√3; 1,37) et (-√3; 1,37)

[ansset]

bjr,
déjà il faudrait s'assurer que ce soit le bon polynome:
post #1 : P(x)=(1/8)(x²-15)(x²-4)
post #3 :

P(x)=(1/8)(x²-14)(x²-4)
on peut simplifier un peu le calcul de la dérivée seconde en écrivant
P(x)=(1/8)u(x)v(x) avec ( si c'est le premier ? )
u(x)=(x²-15) ( le premier facteur donné dans l'énoncé )
v(x)=(x²-4) d'où
u'(x)=v'(x)=2x et
u"(x)=v"(x)=2 donc ( si on oublie le facteur 1/8 )
la dérivée seconde de u(x)v(x) vaut donc u"(x)(u(x)+v(x))+2u'²(x) soit
12x²-38 ( on aurait 36 avec le second énoncé ).
la fin est triviale.

[jacknicklaus]

coordonnées (√3; 1,37) et (-√3; 1,37)

non, encore une fois, en maths on traite avec des nombres exacts, pas avec des approximations à 3 décimales.

tu dois calculer f(√3) de manière exacte.