questions et aide convertir equation paramétrique/cartesiènne

[invite5e477e03]

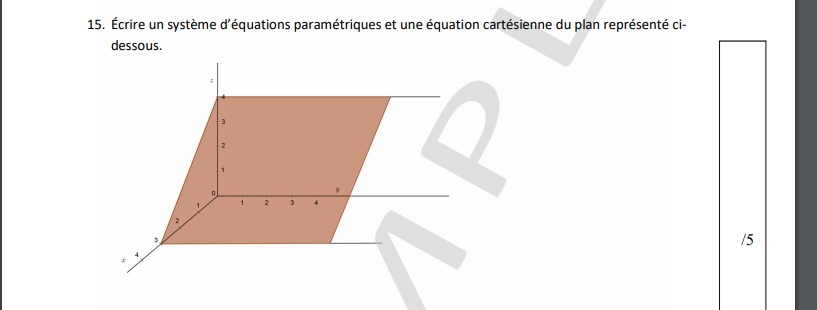
Bonsoir, voici l'exercice que j'essaie de résoudre:



voici comment je procède,merci de me dire si ce n'est pas correct:

j'identifie un point a sur le plan a(0,0,4)
j'identifie ensuite 2 autre point==> b(3,0,0) et c(3,1,0)
je calcule les coordonée des vecteur ab et ac, ab(3,0,-4) et ac(3,1,-4)
les 2 vecteurs ne sont pas colinéaire donc le point a et les vecteurs ab et ac forme un plan:
x=0+3k+3m
y=0+0k+1m
z=4-4k-4m

premièrement, est-ce correct jusqu'ici ?
deuxièmement,si oui, comment convertir cette équation en équation cartésiènne ? merci.
-----

[invite5e477e03]

je me rends compte que j'ai peut etre fait une erreur avec mes vecteurs directeur, ne faudrait il pas , a partir du point a (0,0,4), additionner les vecteur directeur en nombre de fois le déplacement unitaire tel que v1(1,0,-1) et v2(0,1,0) comme les 2 vecteurs fesant l'angle droit au point a ?
et donc :
x=0+1k+0m
y=0+0k+1m
z=4-1k+0m

quelle est la bonne solution entre celle-ci et celle du message précédent ? merci de votre aide.

[invitedb5bdc8a]

deuxièmement,si oui, comment convertir cette équation en équation cartésiènne ? merci.

en éliminant les paramètres k et m pour obtenir une seule équation en x y et z. ici c'est très simple puisque le plan est parallèle à l'axe des y.

NB ton vecteur v1 est faux.

[invite5e477e03]

en éliminant les paramètres k et m pour obtenir une seule équation en x y et z. ici c'est très simple puisque le plan est parallèle à l'axe des y.

NB ton vecteur v1 est faux.

peux tu me dire quelle est la bonne équation du vecteur v1 car je ne comprends pas pourquoi le mien est incorrect: en partant du point a(0,0,4) pour avoir un vecteur décroissant de pente 1 c'est bien v1(1,0,-1) je descend de 1 sur l'axe z et j'avance de 1 sur l'axe x.

j'ai essayé de convertir mon équation en équation cartésienne pour voir a quoi ressemble mon plan sur un graphique, mais je bloque:
j'additionne la ligne 1 et la ligne 3 pour enlever les k
x=0+1k+0m
y=0+0k+1m
z=4-1k+0m

x+z=4
y=m

et la je ne vois pas comment continuer.

merci de votre aide.

[A voir en vidéo sur Futura]

[invite5e477e03]

je pense avoir trouver l'erreur, le vecteur v1 doit etre de coordonnée v1(3,0,-4) et v2 reste le même v2(0,1,0)

ensuite je remplace m par y dans
(4/3)x-0y+z=4

sur mon logiciel geogebra, la plan correspond si ce n'est que il continue vers les y négatif, est-ce une erreur ?

voici l'image, le bon plan est en vert

[invitedb5bdc8a]

oui c'est bon, tu as l'équation du plan et oui, il est infini donc il s'étend sur tous les y, y compris négatifs. Un plan est infini.
Pour représenter un rectangle fini il faudrait rajouter des conditions sur y (0<=y<=6 par exemple) mais ce n'est pas ce qui est demandé.