Bonsoir,
J'ai quelque peu honte de bloquer sur ce sujet d'oral de CAPES de maths de niveau collège/lycée
1/ Analyser les productions des 3 élèves.
2/ Résoudre l'exercice.
L'élève 1 n'a donné qu'une conjecture donc insuffisant.
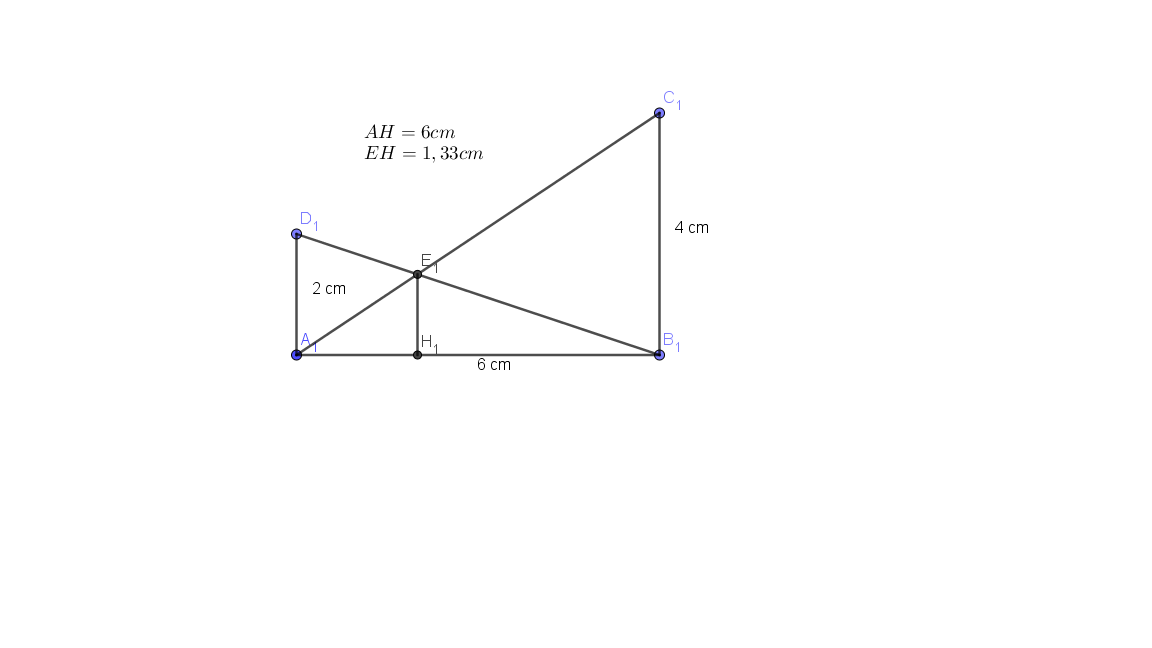
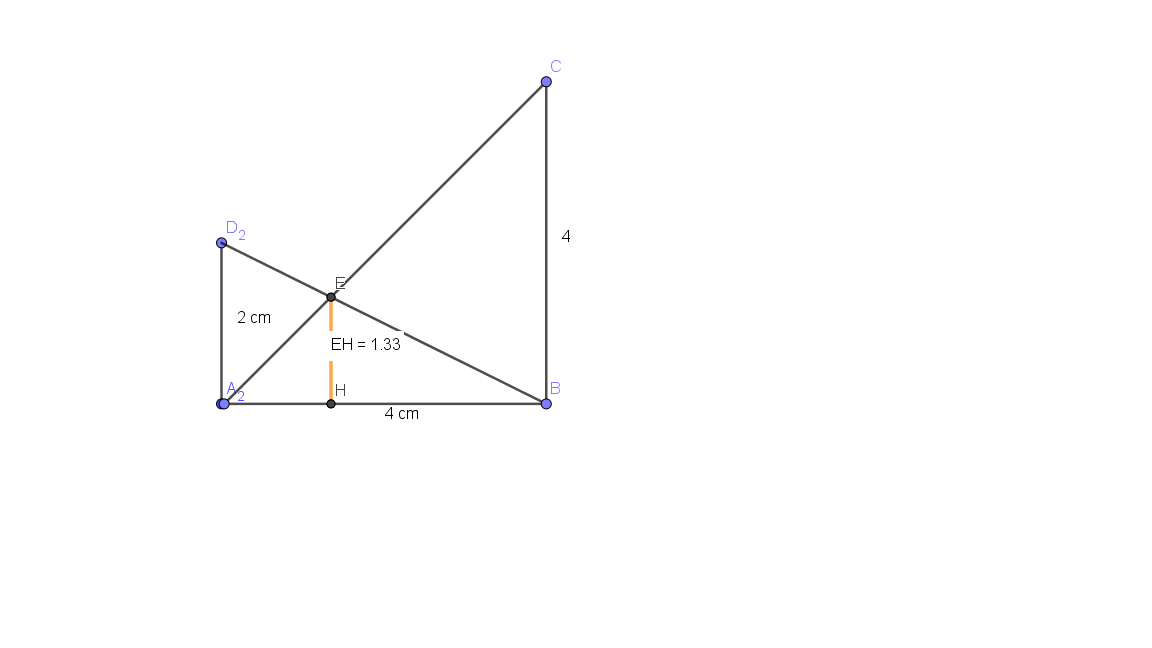
L'élève 2, il a oublié de citer le théorème de Thalès. Mais pour la suite je suis en plein doute :
On a bien AB diminue alors AH diminue. Mais si les 2 termes d'une fraction diminuent, on peut pas savoir lequel diminue le plus donc comment savoir si EH augmente, diminue ou reste constant ?
Pour l'élève 3, je ne sais même plus comment trouver l'équation d'une droite dans un repère qui n'est pas de la formeje ne sais plus comment faire dans un repère
Mais je dirais que sa méthode est fausse car A et B sont fixes dans le repèredonc il ne peut pas étudier les coordonnées de E quand A et B se rapprochent...
-----