Fonction avec parametre m.

[Matlabo]

Salut;

j'ai la fonction f_m(x) = (m-2)x³ - mx + 2............... m ‡ 2

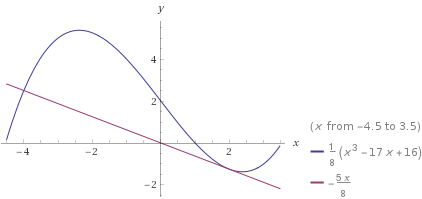
On nous demande d'étudier la position de la courbe C f_m par rapport à la droite dont l'équation est y = -mx+2

Biensûr pour faire cette étude il faut étudier le signe de f_m(x) - y ce qui va donner (m-2)x³

Mais comment étudier le signe de (m-2)x³, la réponse la plus simple serait de faire varier la valeur de x sur tout le domain de définition et prendre m sur ]-inf ; 2[ puis faire varier la valeur de x sur tout le domain de définition et prendre m sur ]2 ; +inf[ Mais je reste perplexe....

Merci!
-----

[invite51d17075]

bjr, cela revient simplement à regarder le signe de le fonction f(x)=ax³ en fonction de a.
a<0 ( soit m ? ) => signe de f(x) selon x ?
a=0 ( m=?) =>même question
a>0 ( m ? ) => idem

[Matlabo]

bjr, cela revient simplement à regarder le signe de le fonction f(x)=ax³ en fonction de a.
a<0 ( soit m ? ) => signe de f(x) selon x ?
a=0 ( m=?) =>même question
a>0 ( m ? ) => idem

ahh...oui j y'avais pas pensé................Merci!

[Matlabo]

Mais, enfaite bahhh c'est bien ce que j'ai proposé ? ?

[A voir en vidéo sur Futura]

[gg0]

Oui,

mais avec perplexité !! On ne sait pas pourquoi.

Cordialement.

[invite51d17075]

-en oubliant le cas m=2
-et sans conclure non plus selon les cas

[Matlabo]

Oui, moi-même je ne sais pas pourquoi je suis perplexe

en sachant que y est l'équation de la tangente à la courbe de cette fonction f qu en déduire de l'étude précédente?

Personnellement je ne vois pas que déduire! À moins pour par exemple m appartient à un certain intervalle et x appartient à un autre intervalle f est supérieur à y...... et on continue comme ça.... jusqu'à terminé tous les cas?¿

[Matlabo]

Aaa... puisque T est la tangente à la courbe au point A et que T traverse la courbe de la fonction f alors A est le point d'inflexion.!!

[invite51d17075]

Salut;
j'ai la fonction f_m(x) = (m-2)x³ - mx + 2............... m ‡ 2
On nous demande d'étudier la position de la courbe C f_m par rapport à la droite dont l'équation est y = -mx+2

Dans ce cas y n'est pas la tangente à la courbe fm(x) en général ( est ce au point A que tu vient de citer ? )
J'ai donc du mal à interpréter cette question.

bref, l'énoncé initial serait utile

[invite51d17075]

f_m(x) = (m-2)x³ - mx + 2............... m ‡ 2

qu'est ce cela veut dire ?

[Matlabo]

Dans ce cas y n'est pas la tangente à la courbe fm(x) en général ( est ce au point A que tu vient de citer ? )

Oui, y est l'équation de la Tangente au point A de la courbe de la fonction f_m..........DESOLE de l'IMPRECISION..


m ‡ 2 : m n'est pas égale à 2......je l'ai écrit avec l'Alt code c'est peut être pour ça.



J'ai un autre probleme:

Enoncé: f_m est une fonction définie sur R, f_m(x) = (m-2)x³ - mx + 2, avec m un paramétre réel différent de 2.

Question: Combien de Tangente à la courbe Cf_m qui passe sur le point O(0;0) .

Bon, on a:

y= f'_m(a)(x-a) + f(a)= ( 3a²(m-2)-m ) (x-a) + (m-2)x³ - mx + 2

on pose g(x) = y

pour passer sur le point (0;0), faudrait que g(0) = 0

g(0) = f'_m(a)(-a) + f(a)= ( 3a²(m-2)-m ) (-a) + (m-2)x³ - mx + 2 = 0


On doit donc résoudre ceci:
( 3a²(m-2)-m ) (-a) + (m-2)x³ - mx + 2 = 0

Comment l'a résoudre??. Le problème c'est qu'on a 2 inconnues ou variables ..... (enfin le m c'est le paramètre ....) ALORS Comment faire ??

Si on avait pas le m ce serait plus simple, .......

[Matlabo]

j'ai mis x au lieu de a ......

Bon, on a:

y= f'_m(a)(x-a) + f(a)= ( 3a²(m-2)-m ) (x-a) + (m-2)a³ - ma + 2

on pose g(x) = y

pour passer sur le point (0;0), faudrait que g(0) = 0

g(0) = f'_m(a)(-a) + f(a)= ( 3a²(m-2)-m ) (-a) + (m-2)a³ - ma + 2 = 0


On doit donc résoudre ceci:
( 3a²(m-2)-m ) (-a) + (m-2)a³ - ma + 2 = 0

Comment l'a résoudre??. Le problème c'est qu'on a 2 inconnues ou variables ..... (enfin le m c'est le paramètre ....) ALORS Comment faire ??

Si on avait pas le m ce serait plus simple, .......

On doit donc résoudre ceci:

( 3a²(m-2)-m ) (-a) + (m-2)a³ - m + 2 = 0

[jacknicklaus]

( 3a²(m-2)-m ) (-a) + (m-2)a³ - m + 2 = 0

non. c'est :


3a²(m-2)-m ) (-a) + (m-2)a³ - ma + 2 = 0


tu développes et tu isoles a³ = .... fonction de m ....

[invite51d17075]

Ce n'est pas l'équation de ta tangente au point (a,f(a))




et en simplifiant

donc de la forme a'x+b'
<=>

[invite51d17075]

mais je ne comprend plus le rapport avec :

On nous demande d'étudier la position de la courbe C f_m par rapport à la droite dont l'équation est y = -mx+2

ni cela en plus :

en sachant que y est l'équation de la tangente à la courbe de cette fonction f qu en déduire de l'étude précédente?

je me demande quel est l'énoncé exact .

[invite51d17075]

en fait, il y avait deux questions différentes, c'est ça ?

[invite51d17075]

OK, deux questions, donc
1) A de coord (0;f(0))=(0;2)
y est tangente en CE point pour tout m diff de 2et aussi point d'inflexion
2) trouver les tgt possibles pour a qcq passant par (0,0)
objet de ma réponse au post#14

[Matlabo]

non. c'est :


3a²(m-2)-m ) (-a) + (m-2)a³ - ma + 2 = 0


tu développes et tu isoles a³ = .... fonction de m ....

Oui, mais j'aimerais savoir comment est ce que ça va m'aider ??...

Ce n'est pas l'équation de ta tangente au point (a,f(a))




et en simplifiant

donc de la forme a'x+b'
<=>

Comment avez-vous fait pour simplifier?



Et pourquoi ce n'est pas l'équation de ta tangente au point (a,f(a)), j'ai vérifié c'est la même chose : 3a²(m-2)-m ) (-a) + (m-2)a³ - ma + 2 =






J'ai distribuer ce qui est dans les parentheses puis j'ai sorti le a^3 ..... et j'ai eu:





Bon mais je ne vois toujours pas comment déterminer combien de Tangente à la courbe Cfm passe sur le point O(0;0)

..............Normalement le nombre de valeur de a qu'on peut trouver est le nombre de Tangente à la courbe Cfm qui passe sur le point O(0;0), N'est ce pas ????


Merci!!! !!

[Matlabo]

J'ai distribuer ce qui est dans les parentheses puis j'ai sorti le a^3 ..... et j'ai eu:





Bon mais je ne vois toujours pas comment déterminer combien de Tangente à la courbe Cfm passe sur le point O(0;0)

..............Normalement le nombre de valeur de a qu'on peut trouver est le nombre de Tangente à la courbe Cfm qui passe sur le point O(0;0), N'est ce pas ????

ERREUR!!!

On va trouver :


Et non pas:





Si on isole le a^3 on obtient:

[invite51d17075]

ERREUR!!!

On va trouver :
Et non pas:

le premier est faux et je n'ai jamais écrit le second mais
-2(m-2)a^3+2=0.
et je pense qu'on cherche les m possibles ( donc les fonctions fm possibles en fct des a, pas l'inverse.)

[Matlabo]

le premier est faux et je n'ai jamais écrit le second mais
-2(m-2)a^3+2=0.
et je pense qu'on cherche les m possibles ( donc les fonctions fm possibles en fct des a, pas l'inverse.)

Mais -2(m-2)a^3+2 = (2-m)a^3 +1 = 0

Et je dois avouer que je n'est pas bien compris ce que j'ai mis en gras??¿ Et comment le faire ?

[invite51d17075]

j'avais lu trop vite. ( pas vu le m-2 au lieu de 2-m )
c'est la bonne équation celle là.
soit (m-2)=1/a^3 donc m=2+1/a^3 (*)
donc qcq a dans R, il existe un m unique tel que
fm(x) est tangente en (a;f(a)) et passe par (0;0).

ex: a=2 ; m=2+1/8=17/8 et
f₂(x)=(1/8)x^3-(17/8)x+2
T_2(x)=-(5/8)x


(*) on voit bien que m doit être diff de 2 ( car ne correspond à aucun a )
on voit aussi le point d'inflexion de la tangente en (0;2) ( première question )

[invite51d17075]

ps : j'ai pris a=2 par hasard , rien à voir avec le fait que fm(0)=2 qcq m.
tu peux refaire un autre graphique avec un autre a.
et je voulais dire précédemment la tangente fm(x) en (a,f(a)) passe par (0;0)

[Matlabo]

c'est la bonne équation celle là.
soit (m-2)=1/a^3 donc m=2+1/a^3 (*)
donc qcq a dans R, il existe un m unique tel que
fm(x) est tangente en (a;f(a)) et passe par (0;0).

ex: a=2 ; m=2+1/8=17/8 et
f₂(x)=(1/8)x^3-(17/8)x+2
T_2(x)=-(5/8)x
Pièce jointe 380289

(*) on voit bien que m doit être diff de 2 ( car ne correspond à aucun a )
on voit aussi le point d'inflexion de la tangente en (0;2) ( première question )

Quel que soit a dans R* ??



Quand vous dites on voit aussi le point d'inflexion de la tangente au point (0;2). Vous l'avez déduit du graphe ou bien de l'équation m= 2+ 1/a^3 ?? Car si c'est de l'équation j'aimerais bien savoir comment?


Donc à chaque fois qu'on va avoir un a et un m qui satisfaient l'équation m= 2+1/a^3 alors on peut dessiner une tangente à la courbe Cfm qui va passer sur le point (0;0).

Et puisqu'il y a une infinité de a et de m qui qui satisfaient cette égalité, alors il y a une infinité de tangente à la courbe Cfm qui passe sur le point(0;0) ???¿

[invite51d17075]

oui pour R*. ( oubli de ma part dans l'écriture mais j'ai précisé qu'on comprenait pourquoi m diff de 2 )
il suffit de dériver deux fois fm(x) ( avec m diff de 2 ) pour montrer qu'il n'existe qu'un seul point d'inflexion en (0,fm(0)=2).
oui, une infinité de tangente, mais une seule pour chaque a.
je ne me souvient plus comment la question était posée.
Cdt

[Matlabo]

Hh, d'accord .

Merci beaucoup!!!

[Matlabo]

Une autre chose :

À vôtre avis comment démontrer qu' il y a une infinité de a et de m qui qui satisfaient cette égalité, et donc démontrer qu'il y a une infinité de tangente à la courbe Cfm qui passe sur le point(0;0) ???

[invite51d17075]

ben, ceci vient d'être démontré justement.
pour tout a non nul
fm avec m=2+1/a^3 satisfait la condition :
la tangente en (a,f(a)) passe par (0;0).
de surcroit g(a)=m est une bijection de R* ds R\{2}
à l'infinité des a correspond une infinité des m

[invite51d17075]

Et l'infinité de tangentes couvre R en entier car
T_a(x)=((-2a³+3a²-1)/a³)x et si
g(x) =(-2x³+3x²-1)/x³ def sur R*
Im(g)=R.
même si la fonction est surjective pour un intervalle.
( c-a-d que plusieurs a peuvent donner le même coeff directeur de la tangente sur cet intervalle)