Déduction du tableau de variation.

[Matlabo]

Salut;

Voila une partie d'un exercice relativement long:

" , Df = R*

K est une fonction définie sur avec

1) Démontrez que K(x²) = [f(x)]² .....C'est fait.

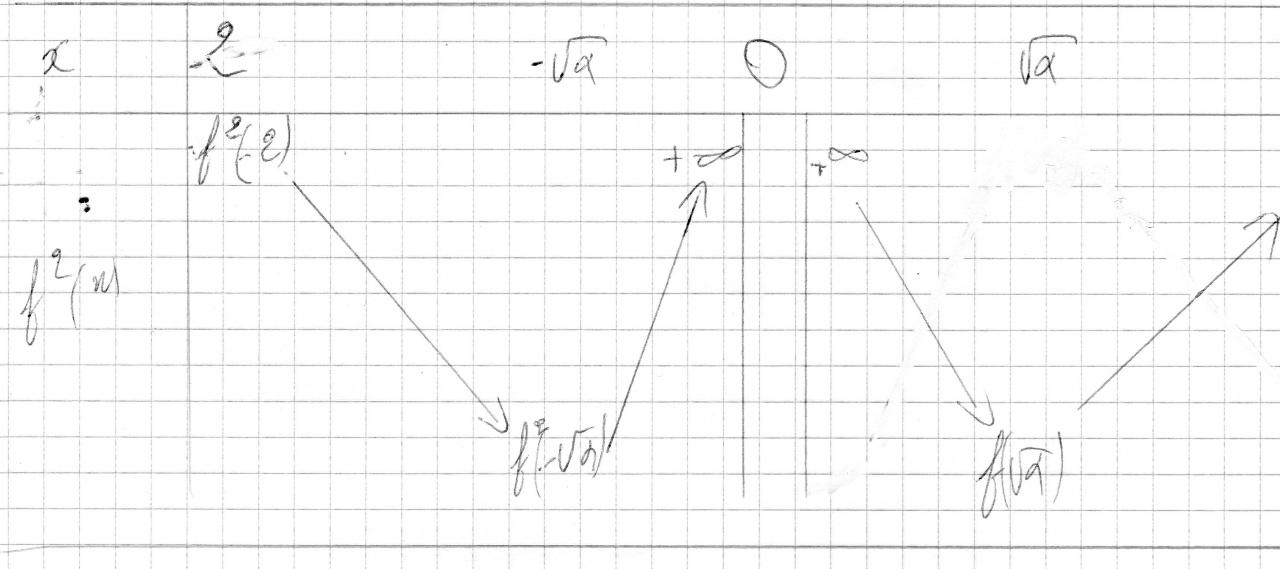
2) Dressez le tableau de variation de la fonction f² sur , puis déduisez le tableau de variation de la fonction K. "


J'ai un problème avec la 2^éme question:

* Ils demandent de dresser le tableau de variation de f²: Bon il est clair que je peux étudier le signe de sa dérivée, mais est-il possible de trouver le tableau de variation de f² en partant de celui de f.

* Puis on nous demande de déduire le tableau de variation de K, et là je ne sais pas comment m'y prendre.


Donc voila, j’espère avoir bien organiser tout ça et Merci pour vos réponses!
-----

[Matlabo]

Re;
En ce qui concerne ma 1ére question "mais est-il possible de trouver le tableau de variation de f² en partant de celui de f?" je pense avoir trouver la solution et ceux en passant par la composante ...
On met g(x) = x² donc [f(x)]² = g(f(x)) et on déduit le sens de variation de f².

En ce qui concerne ma deuxième requête "" déduire le tableau de variation de K, et là je ne sais pas comment m'y prendre
"" je viens de remarquer qu'étant donné qu'on a K(x²) = [f(x)]² donc K(g(x)) = g(f(x)) et puisqu'on connait le sens de variation de g(f(x)) on connait donc celui de (K(g(x)) et ainsi déduire celui de K(x) !

Dites moi si j'ai faux ou bien si on peut s'y prendre autrement !

[gg0]

Bonjour.

On peut tracer le tableau de variations de f² à partir de celui de f si on connaît le signe de f. Sinon, on a le problème de trouver le sens de variation. Par exemple (x²)² = x⁴ a le même sens de variation que x² qui est positif, mais des sens de variation inverses de -x², alors que x⁴ = (-x²)²; et x⁶ = (x³)² a le même sens de variation que x³ sur R⁺ et le sens inverse sur R^-.
Ensuite, tu as une relation entre K et f² pour les réels positifs, donc tu peux déduire des variations de f² celles de K sur : Lorsque x augmente de 0 à l'infini, x² augmente de 0 à l'infini, donc K(x²) = f(x)² ....

Mais directement de l'un à l'autre, ça ne marche pas, car x² a deux sens de variation et ne prend pas les valeurs négatives.

S'il y a eu des questions avant, il y a peut-être des pistes, mais le sens de variation de f(x)² = K(x²) ne dit rien sur ce qui se passe pour K sur [-2,0[.

Cordialement.

NB : Le fait d'utiliser la fonction auxiliaire g te servira si tu as des éléments de cours sur les variations des composées. Que j'ai traité intuitivement ci-dessus.

[Matlabo]

Est ce possible d'avoir une autre manière de résoudre ma deuxième question " déduire le tableau de variation de K " car j'ai eu quelques complications pour trouver les bons intervalles dans le sens de variation de K...

Merci

[A voir en vidéo sur Futura]

[Matlabo]

ah je n ai pas vu le dernier post

[invite51d17075]

bjr,
qu'obtiens tu déjà pour la première, je ne suis pas certain de ta méthode. ( un doute )
pour la 2) je ne comprend pas ta démarche

[gg0]

Pour la question 1, pas de problème.

En fait, ici, il est facile de voir le signe de f, d'autant qu'elle est impaire; elle est de signe constant sur chacun des intervalles de son domaine de définition. Ce qui ne simplifie pas les questions.

Cordialement.

[Matlabo]

Voila ce que j'ai obtenu:




Je n'est pas bien compris ce que vous dites dans le post #3, et oui j'ai des éléments de cours sur les variations des fonctions composées.

Pouvez-vous trouver le sens de variation de K avec les éléments de la composition de fonctions et le tableau de variation de f² que j'ai mis en haut dans le 1er intervalle (de -2 à racine de a) juste pour comprendre puis je continuerai les autres intervalles.

Merci.

P.S: Ma démarche dans la 2 est de trouver le sens de variation de K avec la notion de composition de fonction car on a K(g(x)) = [f(x)]² avec g(x) = x².

D'habitude On a le sens de variation de K et de g puis on trouve celui de kog mais la On a le sens de variation de Kog (en l’occurrence f²) et le sens de variation de g et on veut en déduire le sens de variation de K.

[invite20155811]

Bonjour
Comment as-tu trouvé le tableau de variations de f²

[gg0]

Qui est ?

[Matlabo]

Dans le poste #1 j'ai dis que l'exercice était relativement long et ils nous ont entre autre demandé de trouver le sens de variation de f chose que j'ai faite en calculant la dérivée, pour le alpha il a été donné dans l'ex. f'(alpha) = 0, puis le sens de variation de f² je l ai trouvé avec la notion de composition de fonction mais ça peut aussi se faire avec la dérivée de f².

[Matlabo]

Donc si quelqu'un sait comment trouver le sens de variation de K en partant de g et de f² sachant que [f(x)]²= Kog(x) ou K(g(x))..?

[gg0]

Sur pas de problème (relis le message #3), mais comme x² ne prend pas les valeurs entre -2 et 0, on ne peut rien conclure.

[Matlabo]

Ok pour le mais faut sur tout l'intervalle demandé c'est pour ça que je cherche réponse à ma question post #12

Merci.

[invite51d17075]

bsr,
je ne sais s'il y a eu d'autre question préalables.
mais, clairement , on ne peut "déduire le tableau de variation de K" pour x <0 à partir des seuls éléments mis plus haut.
s'il n'y a rien d'autre, on peut néanmoins étudier la fct K sur [-2;0[ , on observant déjà par exemple que
K(-1)=K'(-1)=0....