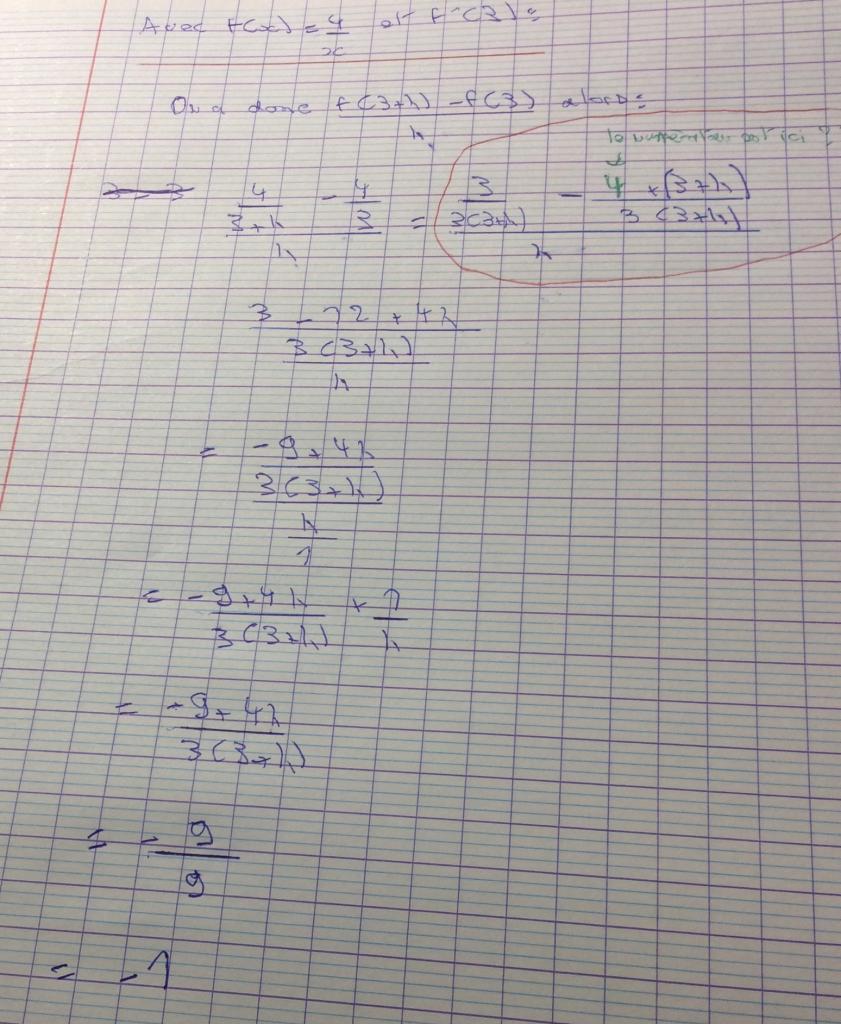Bonsoir je voudrais vous demander de l’aide sur la méthode de calcule de la fonction inverse ci-dessous :
Je ne comprends rien à la méthode dont particulièrement la première étape du calcul et l’apparition du h/1 inversé ensuite en 1/h ??
Si quelqu’un peut m’expliquer ceci avec un vocabulaire très facile et très clair je le remercie !
Ps: Comment on fait cette méthode si le dénominateur de la fonction inverse est autre que 1 ?
bsr:
ici , on applique simplement la définition de la dérivée en un point a=3 soit
mais ici la fonction est f(x)=1/x
donc f(h)=1/h et f(3+h)=1/(3+h).
ensuite ce ne sont que des calculs pour mettre sous la forme a(h)/b(h).
et on obtient a=-1 et b(h)=3(3+h)
puis on fait tendre h vers 0.
je ne comprend pas la question.Ps: Comment on fait cette méthode si le dénominateur de la fonction inverse est autre que 1 ?
Bonjour.
Ce sont les opérations de base avec les fractions
De manière générale, on a :
Diviser par une fraction revient à multiplier par l'inverse de cette fraction. Dans ton cas, "diviser par h/1 revient à multiplier par 1/h".
A noter que le premier "1" n'est pas utile ici : "Diviser par h revient à multiplier par 1/h".
Cordialement,
Duke.
Bonjour merci beaucoup pour vos réponses ! Cependant je ne comprends toujours pas la logique de la méthode . L’autre question que j’ai posé reflétait sur un numérateur ( J’avais confondu avec dénominateur..)de la fonction inverse autre que 1 (Exemple 3/x, 5/x etc...)
Si quelqu’un peut me faire une démonstration en expliquant les étapes sans vouloir forcer me fera le plus grand bien ! Merci d’avance
Dernière modification par Lachimiecphysique ; 10/11/2019 à 11h11.
Bonjour.
"la logique de la méthode" est d'obtenir le résultat par application des règles élémentaires du calcul et de la définition du nombre dérivé en a d'une fonction f. As-tu au moins regardé et appris cette définition ???
Pour la fonction x-->3/x, tu reprends le même calcul que dans le document, en utilisant 3/x à la place de 1/x. Il n'y a aucun mystère, on se contente d'appliquer la définition du nombre dérivé de f(x) en x=3. Si tu veux le nombre dérivé en une autre valeur, par exemple -5, tu remplaces 3 par -5, simplement tu appliques la définition du nombre dérivé.
En fait, soit tu comprends quelles règles ont été appliquées dans ton document du message #1, et tu sais tout, soit il faut poser la bonne question.
Bonjour merci pour votre réponse, je vous envoie un développement d’une fonction inverse pour mieux vous expliquer mon incompréhension:
Ma question:
Que fait-on du numérateur 4 ?
Merci si vous avez à nouveau le courage de m’aider
Bonjour.
La première chose est de faire des calculs sérieux, pas cette bouillie ! le 4 du 4/(3+h) devient un 3 juste après !!! Ou a été oublié. et il y a encore une énormité ensuite !!
Sinon, bien sûr (règles de quatrième) si tu multiplies le dénominateur 3 par 3+h, tu dois multiplier le numérateur 4 par 4+h.
Si tu fais le calcul correctement, h se simplifie.
Cordialement.
Bonjour merci pour votre réponse. Je me suis entraîné ce matin et je crois avoir enfin compris mais...
Comment trouver le dérivé d’une fonction 1/mx + p comme 1/3x+5.... Il faut faire la même méthode ou les choses se font différemment ?
Merci si vous me répondez une nouvelle fois !
bjr,
la même....(*)
mais on voit vite que comme le numérateur est f(x+h)-f(h) ; le "p" disparait immédiatement.
(*)tu verras plus tard qu'on sait dériver directement ce type de fonctions. mais il est "sain" de connaitre la définition à laquelle on retourne souvent quand la dérivée ne se calcule pas facilement avec des fonctions connues.
ps :
j'ai répondu pour le cas (1/mx)+p.
si c'est 1/(mx+p), il faut appliquer la méthode jusqu'au bout ( le p ne disparait pas )
Bonjour.
Plus tu compliques la fonction, plus le calcul va devenir difficile. Mais on ne pratique pas ainsi, on définit une fonction, la fonction dérivée, et on sait la calculer en fonction des calculs qui donnent f. Puis on calcule sa valeur pour le nombre correspondant.
Cordialement.
Dernière modification par gg0 ; 11/11/2019 à 13h18.
