Bonjour
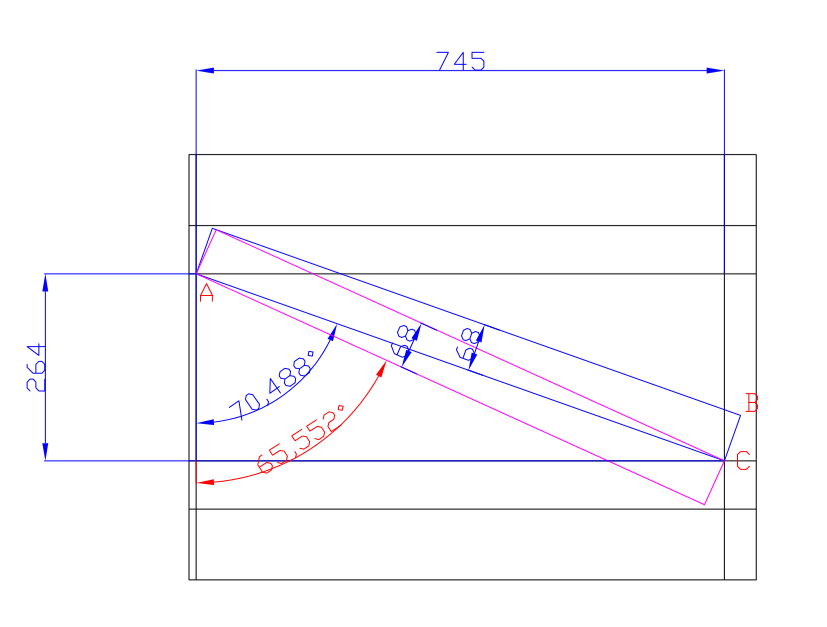
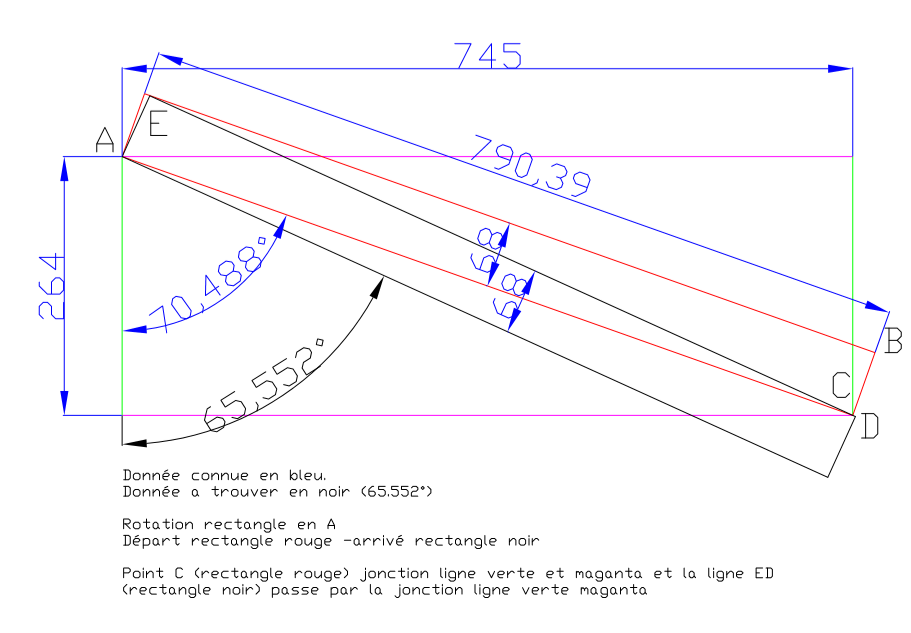
Sur la figure ci joint je connais tout ce qui est en bleu et je veux connaitre la valeur de l'angle en rouge ( ici 65.552°) via un calcul.
En gros un rectangle qui pivote en point A pour que le point B soit au niveau du point C qui est sur la ligne.
Toute aide ou piste sera la bienvenue.
En vous remerciant par avance.
Là c'est plus fort que moi j'arrive pas à resoudre ce problème.
Sonic
bonjour
- Calcule AC en utilisant le cosinus de l'angle en bleu
Soit B' le symétrique de B par rapport à C
- Calcule l'angle en A du triangle CAB' en utilisant l'arcsinus
errata: B' n'est pas exactement le symétrique
Bonjour.
La différence d entre les deux angles (le connu et l'inconnu) est exactement l'angle entre la diagonale du rectangle et le grand côté : Si on appelle D le quatrième sommet (rectangle ACBD) et que la position finale est AB'CD', AC est la diagonale de ce deuxième rectangle. d est l'angle B'AC = BAC.
Tu peux calculer AC avec le théorème de Pythagore, puisque tu as deux autres côtés du triangle don AC est l'hypoténuse, puis, comme tu connais les deux côtés du rectangle ACBD, tu peux calculer l'angle voulu.
Cordialement.
@gg0
Pas d'accord avec "d est l'angle B'AC = angle BAC"
Les 2 rectangles ne sont pas identiques, le rouge est un peu plus court
non, le rouge n'est pas "plus court".
on peut présenter la méthode de gg0 autrement.
la différence d'angle est bien celle que que font les diagonales des rectangles avec leurs grands cotés.
on peut donc raisonner en vecteur avec les coord des points A,B,C
A(0,264)
C(745,0)
et un petit calcul donne celles B:
|CB|=68 et on connait l'angle ( déduit de l'angle en bleu )
ensuite :
etest la diff d'angle entre le bleu et le rouge.
Jall,
il ne faut âs regarder la figure, mais l'explication. Il s'agit d'une simple rotation sur le rectangle.
Cordialement.
ps : avec tes données, je ne retrouve pas tes angles.
ne serait ce que le premier.
Effectivement il faut bien lire l'énoncé et se méfier du schéma.
Le schéma montre le coin inférieur droit du rectangle bleu confondu avec le coin supérieur droit du rectangle rouge (le point C), ce qui est incorrect si on a un rectangle qui a tourné autour de A (Je croyais qu'on avait 2 rectangles de taille légèrement différente ...)
Dernière modification par jall2 ; 17/01/2020 à 13h41.
correction:
je retrouve bien le premier, mais pas exactement le second.Envoyé par ansset
comment l'as tu obtenu ?
En faisant le dessin sur un logiciel de dessin (autocad) qui me demande directement les valeurs.
après vos divers explications, j'ai refait le dessin ( le 1er n'était pas très juste)
j'ai refais mes calculs et je trouve bien la même chose.
et il y a bien plus simple que ce que j'avais suggéré
AC est facile à calculer par pythagore.
de même AB' l'est aussi ( B' étant le bas du rectangle rouge , tj par pythagore )
et AB'/AC donne le cos de l'angle recherché , c-a-d la différence entre les deux angles.
le premier angle ( de 70,488 ) est lui immédiat connaissant les coord de A et C , AOC étant rectangle en O
bonjour
Effectivement la réponse est simple supposons que
le point A est le centre du cercle,rayon= 790.39 environ=> ( racine de (264*264+745*745) (pythagore)
et 68 est la corde
atan(745/264)= 70.488° environ
calcul d'une corde dans un cercle :2*r*sin(angle/2)
r=790.39
corde=68
asin(68/790.39) = 4.935° environ ( difference angle entre 2 rectangles)
et reste qu'à soustraire de 70.488°
soit la formule :
atan(745/264)-asin(68/(racine de (264*264+745*745))) =65.552
atan(longueur/hauteur)-asin(racine de(corde/( hauteur²*longueur²))
a+
