Exercice convexité fonction

[Lachimiecphysique]

Bonjour j’ai besoin de votre aide pour l’exercice suivant:


Partie A:
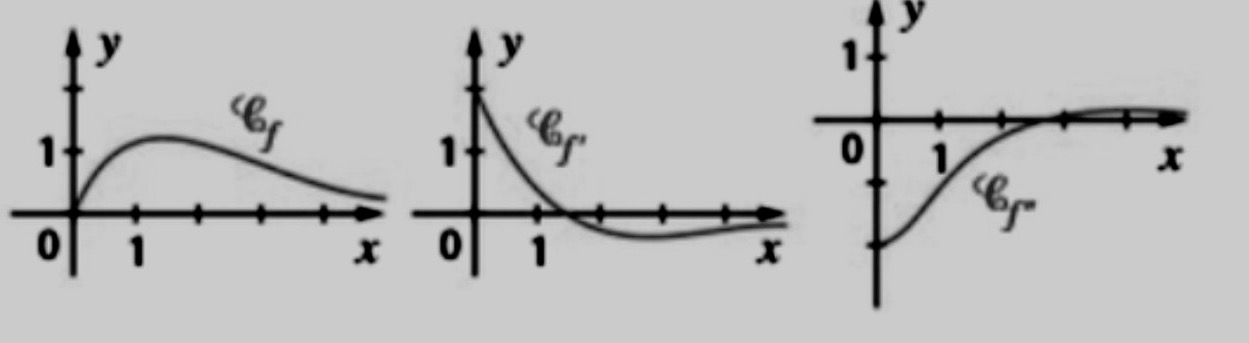
Soit la courbe C_f ci-dessous d’une fonction f définie, deux fois dérivable sur l’intervalle [0;5], ainsi que les courbes C_f’et C_f’’ de f’ et de f’’:
Pièce jointe 426834
Dans cette partie les réponses seront obtenues graphiquement .
a) Donner un intervalle défini par deux entiers sur lequel la fonction f semble convexe.
b) Pourquoi peut-on conjecturer que la courbe Cf admet un point d’inflexion I? Donner un encadrement par deux entiers consécutifs de l’abscisse de I.

Partie B:
On avoue que la fonction f représentée ci-dessus est définie sur l’intervalle [0;5] par f(x) = (x²+2x)e^-x

a) Calculer f’(x) pour tout réel x de [0;5].
b) Montrer que pour tout réel x appartenant à l’intervalle [0;5] que f’’(x)=(x²-2x-2)e^-x.
c) Déterminer sur quel intervalle de [0;5], f est concave.
d) Déterminer les coordonnées du point d’inflexion de Cf sur [0;5]

Partie C

Soit une autre fonction définie sur R avec un réel m:
f(x)=(x²+(m-1)x+3m-1)e^-x
Déterminer les valeurs du réel m pour lesquelles la fonction f est convexe sur R.

Mes réponses :

Partie A :
a)D’après le graphique n°3 f’’ semble positif sur ]2,5;5], donc f est convexe sur ]2,5;5]
b) On peut conjecturer que la courbe Cf admet un point d’inflexion où passe une tangente entre ]2,5;3[

Partie B:
a) f(x)= (x²+2x)e^-x
Ici (uv)’x = u’(x)* v(x) + u(x)*v’(x)
*u’(x)=2x+2. *v’(x)= -e^-x
*u(x) = x²+2x *v(x)= e^-x
Donc f’(x) = (2x+2)*e^-x+(x²+2x)* -e^-x
= e^-x*(2x+2-x²-2x)
= e^-x(2-x²)

b) Ici (uv)’(x) = u’(x)*v(x)+u(x)*v’(x)
*u’(x) = -e^-x *v’(x)=-2x
*u(x)= e^-x. *v(x) = 2-x²

Donc f’’(x) = -e^-x*(2-x²) + e^-x*(-2x)
f’’(x)= e^-x(-2x-(2-x²))
f’’(x)= e^-x(-2x-2+x²)
Donc f’’(x)= (x²-2x-2)e^-x

c) f’’(x) = (x²-2x-2)e^-x
(x²-2x-2)e^-x=0

*x²-2x-2=0
delta = b²-4ac
=(-2)²-4*1*(-2)=12

x1= 2-racine de 12/2*1 = 1-racine de 3
x2= -2+racine de 12/2*1 = 1+ racine de 3

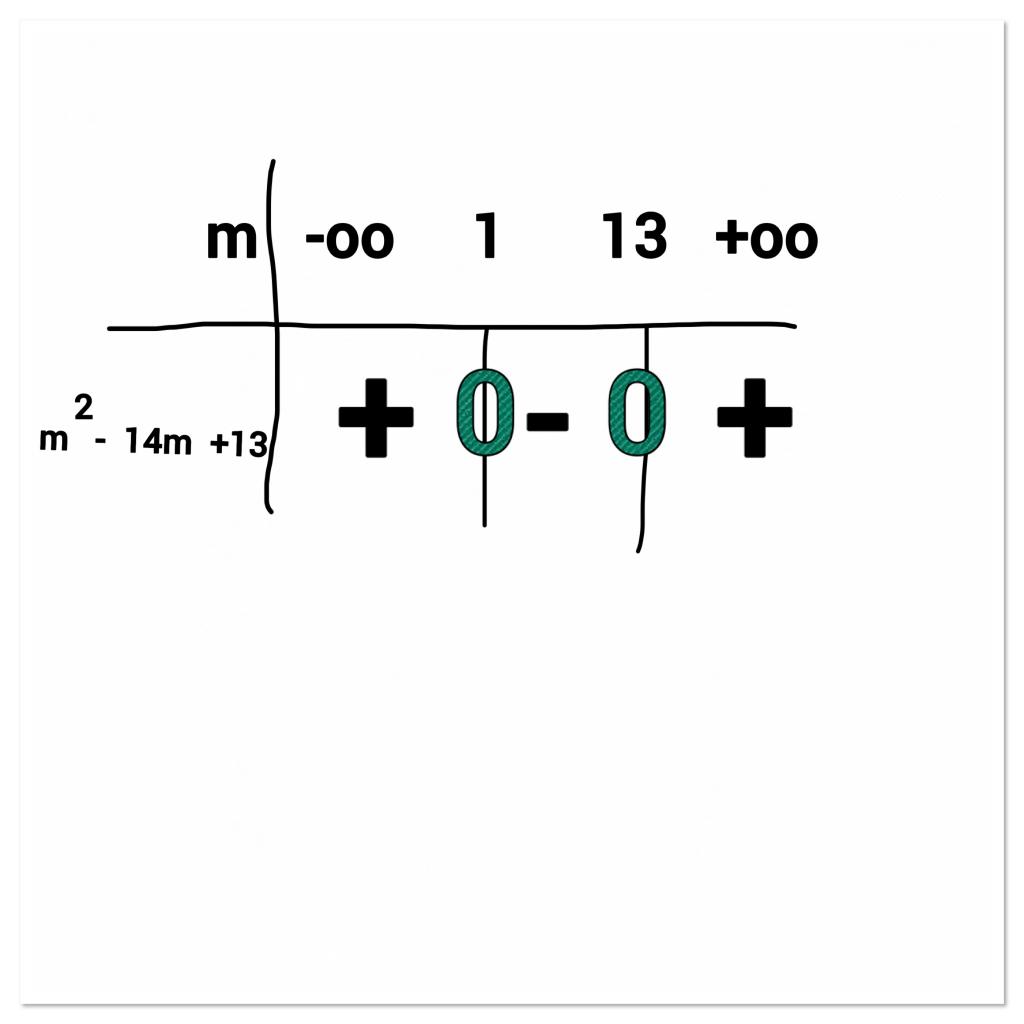
Nous avons donc le tableau de signe suivant sur [0;5]:

17CE9A93-765D-4734-B2F8-6B1EFAD53224.jpg

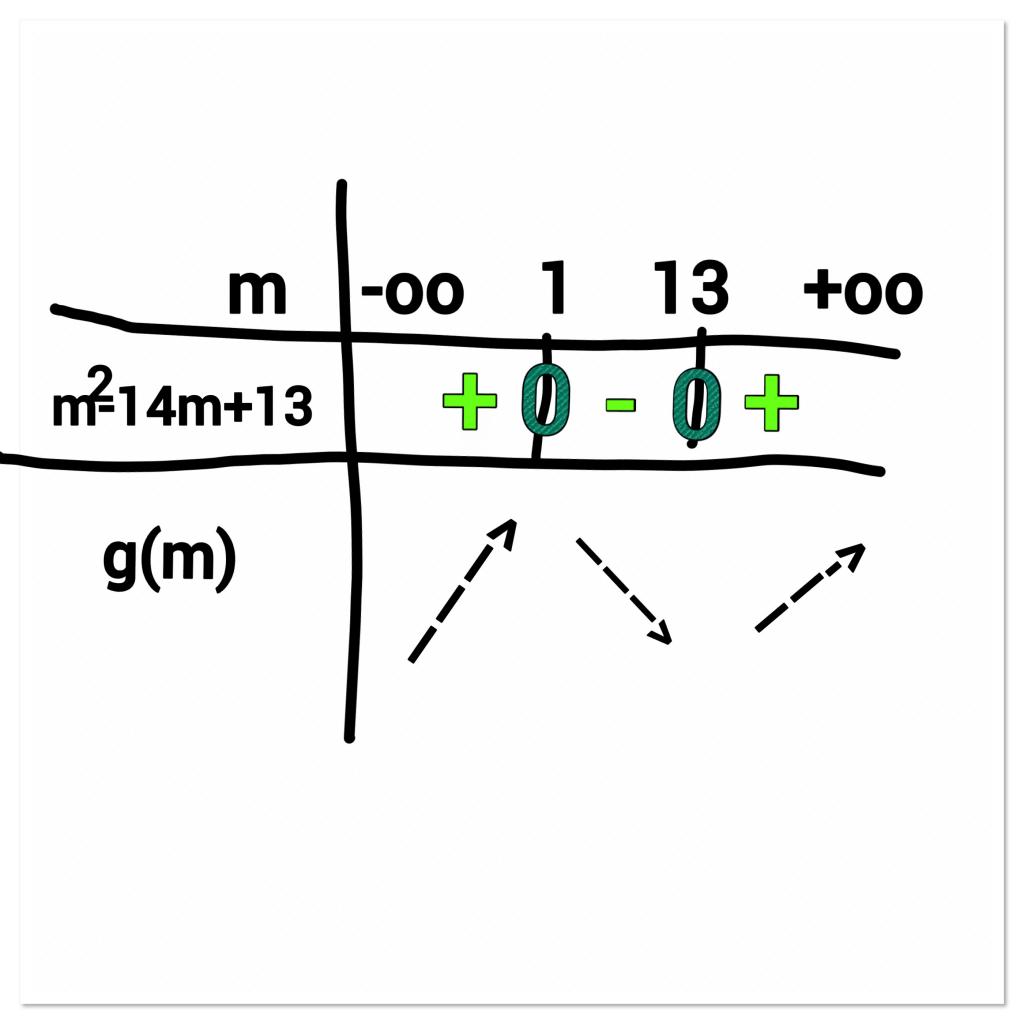
On a donc le tableau de variations suivant :

CF4BEAA3-FB08-438B-A3E3-9EF82EF42B02.jpg

-Alors : f’’ est négative sur [0;1+racine de 3[
-f’ est décroissante sur [0;1+ racine de 3[

Donc f est concave sur [0;1+racine de 3[

d) f’’ s’annule en x=1+racine de 3, en changeant de signe alors un point M (x=1+racine de 3, f(1+racine de 3) ~0,84) est un point d’inflexion.
Donc M(1+racine de 3; 0,84)

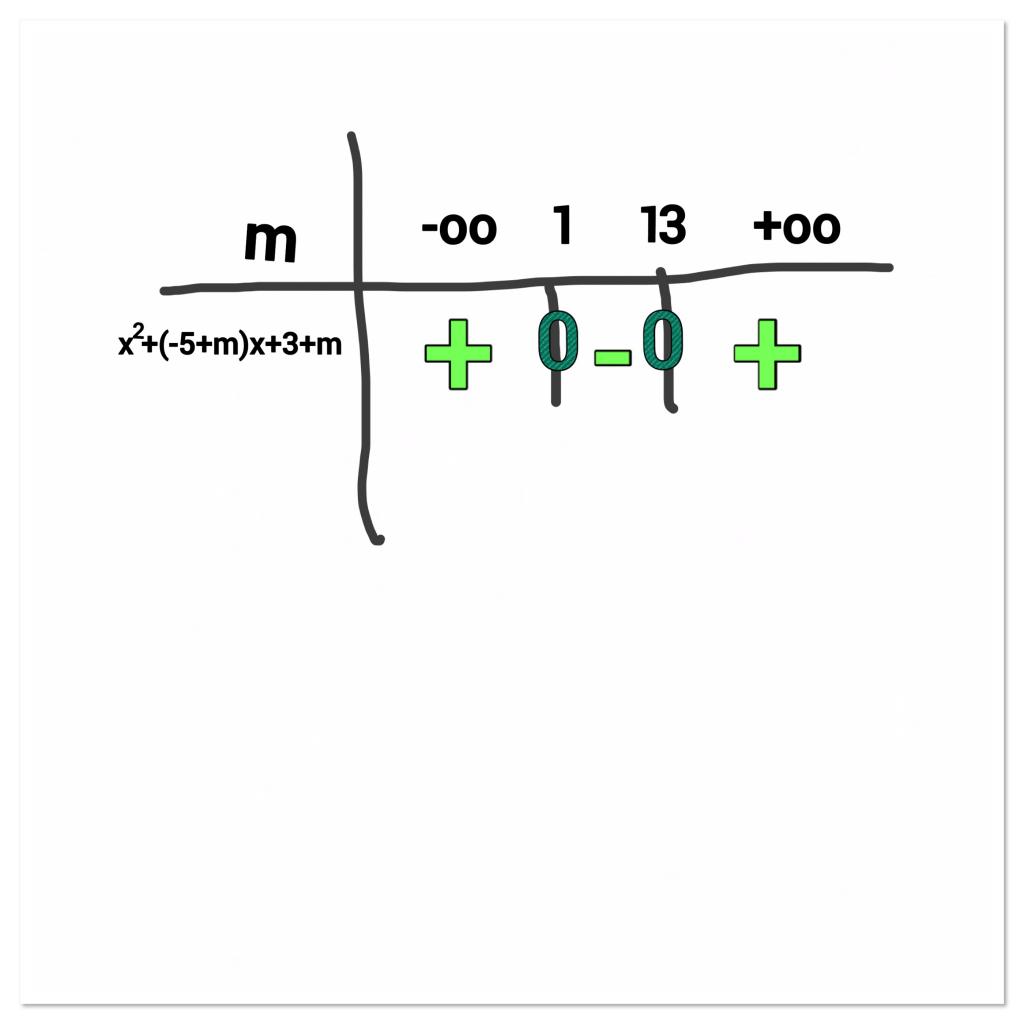
Partie C:

Donc f(x) = (x²+(m-1)x+3m-1)e^-x
Où f’(x) = 3xe^-x-2me^-x-1x²e^-x-1mxe^-x
Où f’’(x) = 3e^-x-5xe^-x+me^-x+x²e^-x+mxe^-x
Alors f’’(x) = e^-x*(3-5x+m+x²+mx)...

Mais comment trouver les valeurs du réel m pour e^-x*(3-5x+m+x²+mx) >0 ???

Merci pour votre aide, bonne journée.
-----

[ansset]

bonjour,
dans la mesure ou ta pièce jointe initiale est illisible ( non valide et donc non accessible ), il est naturellement impossible de te répondre.

[ansset]

re-
donc je t'invite à reposter ta pièce jointe dans un format lisible.

[Lachimiecphysique]

Bonjour, merci beaucoup de votre prévention. La voici :

[A voir en vidéo sur Futura]

[gg0]

Bonjour.

Pour l'essentiel c'est correct.
A, b) Tu ne réponds pas à la question, tu redis ce qu'elle contient.
C : Même méthode que dans les parties A et B pour la première fonction. Ne te laisse pas dérouter par ce m, c'est un nombre.

Cordialement

[Lachimiecphysique]

Bonsoir, merci beaucoup pour votre réponse .
Voici ce que j’ai mis:
A, b) Nous pouvons conjecturer le fait que la courbe C_f admet un point d’inflexion car la dérivé seconde caractérisé par la courbe Cf’’ s’annule et change de signe. Graphiquement je détermine 2,5<xI<3

PARTIE C
[...]
Donc f’’(x) = e^-x*(3-5x+m+x²+mx)
*Ici e^-x ne peut pas être égal à 0.
On a donc 3-5x+m+x²+mx=0
Déterminons le nombre de solutions réelles :
3-5x+m+x²+mx=0
3+(-5+m)x+m+x²=0
Alors x²+(-5+m)x+3+m=0
Ici on peut utiliser delta =b²-4ac car :
*b= (-5+m)
*a=x²
*c=3+m

Donc delta = (-5+m)²-4*1*(3+m)
=(-5)²+(2*(-5)*m)+m²-4*(3+m)
=25-10m+m²-12-4m
=m²-14m+13

On sait que delta = b²-4ac est appliqué par la règle suivante:

*Si delta >0, il a admet 2 solutions
*Si delta =0, il admet 1 solution
*Sil delta <0, on a aucune solution

Tout ceci peut s’exprimer par les 3 inéquations suivantes:

*m²-14m+13>0
*m²-14m+13=0
*m²-14m+13<0

Ici nous pouvons utiliser une nouvelle fois delta = b²-4ac pour résoudre ces 3 inégalités avec un tableau de signe et avec le tableau de variations.

delta = b²- 4ac = (-14)²-4*1*13=144
delta >0, il y a 2 solutions :

*x1 = 14-racine de 144/2 =1
*x2= 14+racine de 144/2 = 13

On a donc pour f’’(x) le tableau de signe suivant :

64BD4AF4-DC91-4876-A52D-582925FBFD20.jpg

On a donc le tableau de variations suivant :

D5DBA877-EB81-48EB-85A6-6020D49FA004.jpg


Donc: -f’’ est positive sur ]-oo;1[U]13;+oo[
-f’’ est croissante sur ]-oo;1[U]13;+oo[

Donc f est convexe sur ]-oo;1[U]13;+oo[

C’est bon ?
Merci pour votre aide.

[gg0]

Tout va bien (sauf le a=x² à la place de a=1 que tu as utilisé) jusqu'à
"On a donc pour f’’(x) le tableau de signe suivant :"
Le signe de f" n'est pas celui de m²-14m+13.
D'ailleurs, tu te pièges toi-même en appelant x₁ et x₂ les racines d'un polynôme en m (les appeler m₁ et m₂ aurait été mieux, non ?). Ton premier tableau est ridicule, tu donnes le signe de m²-14m+13, qui ne dépend que de m, en fonction .. de x !!

Il est inutile de faire un calcul si tu ne sais plus pourquoi tu le fais. Reprends et relis ce que tu avais écrit.

Cordialement

[Lachimiecphysique]

Bonsoir merci pour votre réponse et votre correction, voici où j’en suis pour la partie C:

[...] Ici on peut utiliser delta = b²-4ac car:
-b=(-5+m)
-a=1
-c=3+m

Donc delta = (-5+m)²-4*1+(3+m)
=(-5)+(2*(-5)*m)+m²-4*(3+m)
=25-10m+m²-12-4m
=m²-14m+13

On sait que delta = b²-4ac est appliquée par la règle suivante :
-Si delta >0, on a 2 solutions
-Si delta =0, on a 1 solution
-Si delta <0, on a aucune solution

Tout ceci peut s’exprimer par les 3 inéquations suivantes:
*m²-14m+13>0
*m²-14m+13=0
*m²-14m+13<0

On peut donc utiliser une nouvelle fois delta = b²-4ac pour résoudre ces 3 inégalités avec un tableau de signe et pour finir avec un tableau de variations.

Ici delta =(-14)² -4*1*13=144
delta >0, on a donc 2 solutions.

m1= 14-racine de 144/2=1
m2= 14+racine de 144/2 = 13

On a donc le tableau de signe suivant :


Je note f(m)= m²-14m+13

Je n’arrive à voir le rapport entre f(m) et f(x) pour déterminer les valeurs des réels m pour lesquelles la fonction f est convexe sur R ?

Si f(m)>0, alors f’’(x)>0, donc f est convexe sur R??
Donc f est convexe sur ]-oo ;1[U]13;+oo[ ??

Merci pour votre aide, bonne soirée.

[gg0]

Pourquoi appeler f(m) ton deuxième discriminant ? Il n'a rien à voir avec f, que tu étudies.
C'est le discriminant de quoi ? Pourquoi l'as-tu calculé ??? Reprends ton calcul, tu verras bien à quel moment tu reviens à f">0.

Ça ne sert à rien de copier coller un texte alors qu'il faudrait le lire.

[Lachimiecphysique]

Bonjour, merci pour votre réponse.
Voici ce que j’ai essayé de faire :

Je note g(m) = x²+(-5+m)x+3+m=0
delta = m²-14m+13 est le discriminant de g(m), on a donc le tableau de variations suivant:



Mais g(m) fait partie de f’’(x) = e^-x*(3-5x+m+x²+mx) = e^-x*(x²+(-5+m)x+3+m).
En sachant que e^-x sera toujours positif on en déduit que le signe de f’’(x) dépend seulement de g(m).
*Donc quand g(m) est croissante, f’’(x) est positive .
*Quand g(m) est décroissante, f’’(x) est négative.

On sait d’après le tableau de variations que g(m) est croissante sur ]-oo;1[U]13;+oo[, donc f’’(x) est positive sur ]-oo;1[U]13;+oo[ . Donc f(x) est convexe sur ]-oo ;1[U]13;+oo[ selon les valeurs de m.

Merci si vous me corrigez une nouvelle fois, bonne journée.

[gg0]

message supprimé

[gg0]

Combien de temps continueras-tu à ne pas tenir compte de ce que tu as écrit (*) et à raconter n'importe quoi !! Depuis quand les variations du discriminant donnent-elles le signe d'un polynôme.
C'est idiot, tu avais bien commencé, puis tu as dérapé et tu continues à raconter n'importe quoi alors que tu avais dit exactement ce qu'il fallait trouver.

(*) Je te cite :
On sait que delta = b²-4ac est appliquée par la règle suivante :
-Si delta >0, on a 2 solutions
-Si delta =0, on a 1 solution
-Si delta <0, on a aucune solution

Tout ceci peut s’exprimer par les 3 inéquations suivantes:
*m²-14m+13>0
*m²-14m+13=0
*m²-14m+13<0

[Lachimiecphysique]

Bonjour, donc je continue ce que vous avez cité :
[....] On peut utiliser une nouvelle fois delta = b²-4ac pour résoudre ces 3 inégalités :
*Ici delta = (-14)²-4*1*13=144
delta >0, on a donc 2 solutions :
*m1= 14-racine de 144/2 = 1
*m2 = 14+racine de 144/2=13

-Donc m²-14m+13>0 quand m appartient ]-oo;1[U]13;+oo[
-Donc m²-14m+13=0 quand m1=1 ou quand m2=13
-Donc m²-14m+13<0 quand m appartient à ]1;13[.....

Après je ne sais pas quoi faire avec ces renseignements sur m?

Mais j’ai essayé de faire la chose suivante, en modifiant les tableaux de variations et de signes précédemment (mais ça doit être idiot...)
- On a donc pour f’’(x) le tableau de signe suivant :
3A8CD4B2-5C50-459B-9807-D52CBC6848D0.jpg

-On a donc le tableau de variations suivant :
EA380725-60D6-42C2-ABD6-271F65A46082.jpg





Alors : -f’’ est positive sur ]-oo;1[U]13;+oo[
-f’ est croissante sur ]-oo;1[U]13;+oo[

Donc f est convexe sur ]-oo;1[U]13;+oo[..

Merci beaucoup si vous avez encore le courage de m’aider !

[gg0]

"Après je ne sais pas quoi faire avec ces renseignements sur m?" (je n'ai pas lu la suite, aucun intérêt.

Tu as donc trois cas pour m, regarde ce qui se passe dans chacun des trois cas :

* quand m appartient ]-oo;1[U]13;+oo[, m²-14m+13>0. Et m²-14m+13 est le discriminant de x²+(-5+m)x+3+m. Donc tu peux appliquer les règles du cours. Que cherches-tu à propos de x²+(-5+m)x+3+m ? Comme c'est un facteur de f", et que tu cherches le signe de f"(x), ce que tu veux c'est le signe de x²+(-5+m)x+3+m, et tu as une règle de cours à ce propos.

C'est quand même un peu décevant que tu ne sois pas capable de décoder toi même ta propre démarche, et que tu passes ton temps à faire des imitation bêtes d'autres situations. Au lieu d'appliquer les règles du cours. Pourquoi agis-tu bêtement ? Tu es bien plus intelligent que ce que tu fais, arrête !

[Lachimiecphysique]

Bonsoir, merci une nouvelle fois pour votre aide. Voici ce que j’ai fais
[...]

On sait que : x²+(-5+m)x+3+m est un facteur de f’’ où le signe de f’’(x) dépend de ce dernier.
-m²-14m+13 est le discriminant de x²+(-5+m)x+3+m.

Cherchons donc le signe de x²+(-5+m)x+3m avec delta = m²-14m +13

delta = (-14)²-4*1*13=144
delta > 0, on a donc 2 solutions :
*m1 = 14-racine de 144/2=1
*m2= 14+ racine de 144/2 =13

On a donc le tableau de signe suivant pour x²+(-5+m)x+3+m:




En conséquence x²+(-5+m)x+3+m est positive sur ]-oo;1[U]13;+oo[. On sait que ce dernier est un facteur de f’’(x), donc f’’(x) est positive sur ]-oo;1[U]13;+oo[.
Donc m appartient à ]-oo;1[U]13;+oo[ pour que la fonction f est convexe sur R.

C’est bon ?

Merci encore pour votre aide

[gg0]

Bon je renonce. Tu continues à faire n'importe quoi. J'espère seulement que la correction de ton devoir faite par ton prof aura un sens pour toi. Car tu es incapable d'appliquer les règles sur les trinômes, tu risques de ne' pas comprendre quand ton prof les appliquera

Pour montrer à quel point c'est absurde, ce que tu fais, je reprends ta conclusion
Donc m appartient à ]-oo;1[U]13;+oo[ pour que la fonction f est convexe sur R.
Pour par exemple m = 0, qui est bien dans ton intervalle, voici la courbe de f. pas très convexe !!