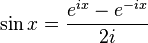Bonjour,
J'ai un problème avec une TF et j'ai beau tourner et tourner je ne vois pas comment y arriver. Il s'agit de la. Je ne vois pas vraiment comment partir. Est-ce que quelqu'un pourrait me dire comment faire ou au moins me donner une piste svp.
Merci beaucoup
ByeBye
Re,
J'ai déjà essayé en décomposant avec euler et j'ai aussi tenté en partant du théorème de la dérive
Je sais juste que je dois arriver à :
Voila
ByeBye
Re,
Alors, j'ai rere....refait avec le théorème de la dérivée et je trouve ça
Et, là je suis bloqué et j'arrive pas à voir comment atterir sur ce que j'ai montré au-dessus.
Une petite idée quelqu'un??? SVP
ByeBye
Bonjour,
Personne n'a une petite idée pour moi ?
svp svp svp
Je veux bien savoir aussi, je cherche sur internet.
Ha c'est bon j'ai trouvé de moi meme l'idée, je poste
ensuite tu dis que:
en ayant posé
or
En parlant de
on a donc , en parlant de TF:
d'où
Voilà, tu fait pareil pour l'autre exponentielle en posant
Ce resultat est juste , car quand tu fais le changement de variable
Donc c'était plutot simple, inutile de sortir les théorèmes de dérivés et compagnie :O
Dernière modification par FonKy- ; 18/01/2009 à 13h41.
Ton résultat selon le signe de la fréquence je ne sais d'ou ca sort.
Sinon pour toi en terme de raisonnement, tu vois bien d'apres le resultat final que ca ressemble énormément à :
Merci beaucoup
Le résultat avec le signe, c'est qu'il y a écrit dans mon cours. Mais, le prof à juste donné la valeur de la TF sans démontrer. En tout cas, ça m'aide beaucoup ce que tu as écrit. MERCI
ByeBye
De rien.
T'es sur qu'il s'agirait pas de la valeur du gain qu'il donne ?
Hola,
Ouais je suis sûr qu'il ne s'agit pas du gain. Je ne sais pas vraiment ce que c'est....
