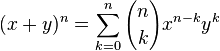Bonjour
J aurais besoin d un coup de main pour avoir une ligne de depart.
Je cherche a demontrer que le produit des longueurs des (n-1) cordes reliant n points d un cercle est egal a n.
Enfin ca c est que pour le contexte. Pour arriver a cela il me faudrait demontrer que (1-w2)(1-w3) ... (1-wn)=n
avec w1=1, w2, w3, ..., wn les racines complexes de 1.
Je cherche une piste de depart ....
Merci beaucoup
Tu peut peut être faire intervenir les angles moitiés de chaque racine
(1-wi) se simplifie alors en factorisant par cos(angle moitié)
On est rapporté à une multiplication de n cosinus et de n exponentielles complexes
Salut,Envoyé par Armellle
Essaie de trouver un polynôme qui a les racines nièmes de l'unité comme racines. Cela t'aidera beaucoup.
bonjour
remarque que
c'est pas plutôt
En fait j'avais essayé de faire w^n=1, d w^n=0 et la j'avais pris un polynome, mais ca m'avance a rien puisque de toute façon c'est égal a 0 (et c'est logique puisque 1 est une des racines n iemedonc ca m'avancait pas ...
Sinon pour les autres, ca fait partie des questions suivantes, donc faut que j'utilise autre chose ...
CERTAIN puisque
Je peux pas m'en servir car c'est un résultat qu'on me demande de prouver dans la question d'parès ....CERTAIN puisque
Une méthode par les polynômes : les racines n-ièmes de l'unité sont racines du polynôme Xn-1, donc les Zi=1-wi sont racines du polynôme (1-Z)n-1
Développe ce dernier polynôme et prend le produit des racines non nulles.
oui excuse moi JUVE ta raison il y a 2 "écritures" :
et aussi
J'essaye, mais je vois pas trop ou ça mène ...
J'arrive à (1-Z)^n -1= (w2*w3*w4*...*wn)-1
Non ta formule n'est pas juste : wi n'est pas racine du polynôme que je t'ai donné.
Il te faut développer le polynôme (1-X)n-1 sous la forme :
(-1)nXn+.....
Les racines de ce polynôme sont exactement les (1-wi), y compris quand wi=1;
Tu divises ce polynôme par X pour obtenir le polynôme dont les racines sont les (1-wi) pour wi différent de 1
En fait je comprend vaguement l'idée mais j'arrive pas à cerner plus ...
Je crois que je vais aller voir avec mon chargé de cours tout à l'heure pour qu'il m'explique (enfin si il veut bien ...)
Merci en tout cas.
Voici l'idée : les wi sont les racines du polynôme Xn-1
Quel est le polynôme dont les racines sont exactement les 1-wi ?
Bah (1-X)^n -1 jusque la j'avais compris :P
Développe le polynôme, le terme constant va disparaître, donc tu vas avoir un polynôme
(-1)nXn+(-1)n-1nXn-1+...+nX
OK ?
Mmmh en fait je ne comprend pas trop comment tu le developpes ...
le binôme de Newton pour (1-X)n ?
Oui c'est ce que j'essaye d'utiliser mais je trouve pas la même chose ^^
Que trouves tu ?
(1-X)^n = n*1^(n-1)*(-X) + (n(n-1))/2 * 1^(n-2)(-X)²+ ....
Regarde bien : ta formule n'est pas valable pour n=2 !
Effectivement, ....
pourtant c'est bien ça
la formule de depart du binome de newton ?
Oui donc tu vas trouver quoi pour k=1 ?
n * 1^(n-1) * (-X)
Ah bon ? Tu es sure que le coefficient binomial Cn1, cela vaut n*(n-1)/2 ?
euh bah pour moi c'est (n!)/(k!(n-k)!)
donc si k=1 (n!)/(1!(n-1)!)=(n!)/((n-1)!)=n non ?
si k=2 (n!)/(2!(n-2)!)= (n(n-1))/2
Ca m'parait logique pourtant, mais je dois me tromper alors ...
Non c'est bon, donc le coefficient de X est -n, et donc il te faut diviser par -X pour enlever la valeur wi=1, je te laisse finir
DOnc ca me ferai
[(1-X)^n]/(-X) = [n*1^(n-1)*(-X) + (n(n-1))/2 * 1^(n-2)(-X)²+ .... ]/(-X)
=n*1^(n-1) + (n(n-1))/2 * 1^(n-2)(-X)+ .... + (-X)^(n-1)
Mais je vois pas quoi faire de ça par rapport a ce que ej cherche à demontrer, je suis un cas désespéré la je crois
Bon en fait l'énoncé n'était pas clair ....
ce qu'il faut montrer c'est que la longueur des cordes d'un cercle de rayon 1 est |1-w2|*|1-w2|* ... * |1-wn|
c'était donc pas des () mais des modules ...
