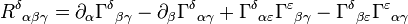aide pour calculer le tenseur de Ricci

[invite930a0644]

Boujour a tous
je suis nouveau dans ce forum, j'ai un probleme dans le calcul de tenseur de Ricci, j'ai calcule le tenseur de Ricci avec les cordonnées sphériques et j'ai trouve tout les éléments de ce tenseur égale a 0 mais malheureusement c'est faut car
R11=-1/r^2
R22=-sin(teta)^2/r^2

y'a t'il persone qui sais comment calculer ce tenseur avec plus de detail
merci
-----

[phys4]

Bon jour,
Je ne connais qu’un type de calcul pour ce tenseur : il faut d’abord calculer les Christoffel à partir des dérivées de la métrique. Puis le tenseur de Riemann est donné par une formule avec 2 dérivées et deux doubles produits des Christoffel (formule un peu longue pour ce forum).
Ensuite le produit par la métrique permet de le contracter en tenseur de Ricci, puis tenseur scalaire qui redonne simplement la courbure de la sphère. Exercice d’entrainement, mais que je n’ai pas sous la main. Je peux retrouver les valeurs.
Utilises tu le même type de calcul ?

[invite930a0644]

merci pour votre réponse mais mon problème est:
1-j'ai calculé les symboles de Christoffel a partir du tenseur metrique des cordonnees spheriques et j'ai trouvé des resultats justes (9 symboles non nulles)

2-j'ai calculé le tenseur de Ricci à partir des symboles de Christoffel

Nous obtenons enfin le tenseur de Ricci par réduction :

mais j'ai trouvé tous les elements de ce tenseur =0

je demande un calcule détaillé
merci a l'avance

[phys4]

Les termes correspondent bien aux coordonnées sphériques avec la métrique g_ΘΘ = r² et g_ΦΦ= r²sin²Θ, la valeur g_rr = 1 n’a pas lieu d’être puisque l’on reste sur la sphère.
Les dérivées en r ne devraient donc pas exister puisque r est une constante dans ce problème.
Il ne devrait donc rester que 3 Christoffel non nuls et deux valeurs.
Г^Θ_ΦΦ = -cos Θ sin Θ
Г^Φ_ΦΘ = Г^Φ_ΘΦ = - cotg Θ
Le calcul en 2D sur la sphère donnera la courbure de la sphère, et le calcul 3D redonnera R = 0 dans l’espace plan. Serait ce aussi simple ?

[A voir en vidéo sur Futura]

[phys4]

Me voici de retour,
J’ai pris le temps de revoir les notations, ce qui m’a montré une erreur de signe sur l’un des termes :
Si l’on tient compte des coordonnées rectangulaires certaines formules se simplifient.
De plus il est possible d’éviter le passage par le tenseur de Riemann en contractant sa formule.
Pour un petit nombre de termes non nuls, le calcul est plus simple. Dans le cas présent, il n’y a qu’un seul terme qui se dédouble.
Métrique à deux dimensions sur la sphère :

[invite06a166f3]

Je suis tout nouveau dans le monde des "hautes" maths et je ne comprends absolument rien de c que vous racontez !
J'essaye de comprendre comment on déduit la valeur des g00 ou g11 mais c'est pas possible pour moi ! D'abord quelqu'un pourrait-il me dire à quoi sert ces tenseurs ?

[phys4]

Bonjour Parouski,

Les coefficients g sont les coefficients de base qui définissent la géométrie des coordonnées.
Ils donnent l'élément de longueur en fonction des variations des coordonnées :

Pour des coordonnées rectangulaires, les termes croisés g_ij sont tous nuls, pour des coordonnées orthonormées les termes g_ii valent 1 (ou -1).
Inversement si les g sont connus en tout point de l'espace, alors la géométrie est déterminée. Ils dépendent généralement des coordonnées. S'ils sont constants en tout point, alors l'espace considéré est plan et il existe une transformation des coordonnées qui permet de revenir à des coordonnées orthonormées. Cependant ce n'est pas une condition nécessaire, car nous pouvons définir des coordonnées curvilignes dans un espace plan.
A partir des g, il possible de calculer les dérivées Г, ces coefficients nous donnent l'accélération d'un mobile en fonction des coordonnées et de son déplacement. Ils permettent de calculer la trajectoire d'un mobile dans un espace quelconque.
Cette géométrie est indispensable pour résoudre les équations de la relativité générale car, dans ces cadre, il n'existe plus de coordonnées orthonormées.