Je dois faire un exercice de math sur les suites mais je n'y arrive pas.
exercice:
Soient a un nombre entier naturel impair et Un une suite de nombres entiers naturels, où U0 est choisi arbitrairement et
Un+1 = Un/2 si n est pair
Un+1 = Un + a si n est impair
Démontrer que Un est périodique à partir d'un certain Uk.
Merci d'avance
-----






 Cela n'a pas de sens d'imposer seulement U0 pair, il faudrait aussi imposer que pour tout n pair, Un est pair.
Cela n'a pas de sens d'imposer seulement U0 pair, il faudrait aussi imposer que pour tout n pair, Un est pair.


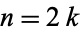 , where
, where 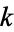 is an integer. The even numbers are therefore ...,
is an integer. The even numbers are therefore ..., 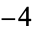 ,
, 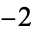 , 0, 2, 4, 6, 8, 10, ...
, 0, 2, 4, 6, 8, 10, ... 