Théorème du Rang

[justine&coria]

Bonjour,

Donc, voilà j'ai une petite question sur le "Théorème du Rang".
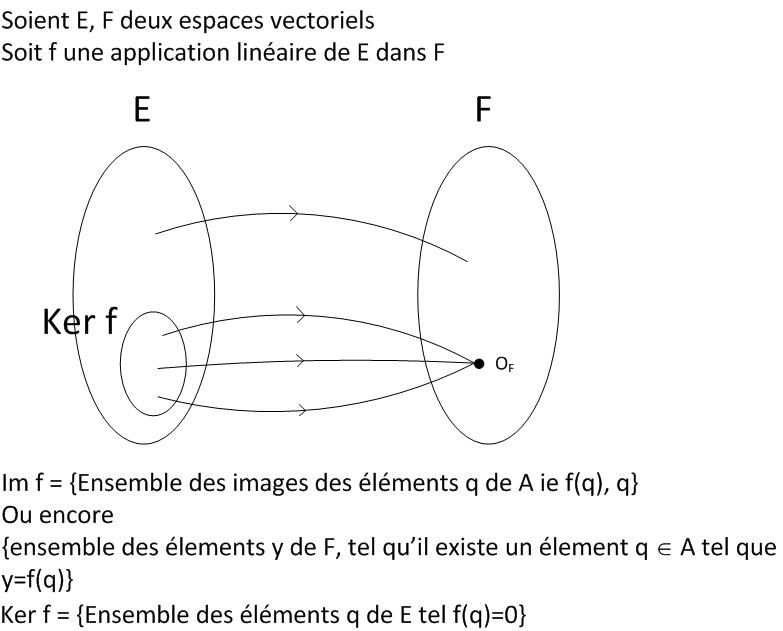
Pour rappel : si f est une application linéaire de E dans F (E et F étant des espaces vectoriels), alors le théorème du rang dit :
dim(E) = dim(Im(f)) + dim(Ker(f)) ou plutôt dim(E)=rg(f)+dim(Ker(f)) (pour faire apparaître la notion de rang dans le théorème portant son nom. )

Bref, en cours, on a vu une démonstration de ce théorème : démonstration très satisfaisante, puisqu'elle démontre (logique !!) ce théorème.

Mais bon, moi j'ai un petit problème. Je suis quelqu'un qui m'imagine les choses pour les comprendre : je le fais pour tout, et ça me permet de mieux comprendre, de mieux retenir les formules, le cours etc.
Et ce théorème, j'arrive pas à me l'imaginer. Pourquoi est-ce que dim(E) serait égal à dim(Im(f)) + dim(Ker(f)) ? J'essaie de comprendre, de me remémorer les définitions des Images, des Noyaux, mais rien n'y fait, je comprends pas pourquoi ce serait le cas !!

Comme je sais qu'ici, il y a des personnes très intelligentes qui ont sûrement compris le pourquoi du comment, j'espère que quelqu'un pourra m'éclairer.
Je ne pense pas que ce soit un théorème totalement contre-intuitif que la raison, l'intuition ne pourrait pas imaginer. Je n'attends pas une démonstration rigoureuse, je demande juste à ce qu'on me l'explique "avec les mains". Bon, d'accord, je sais que ce sera assez dur, mais s'il vous plaît. . J'ai cherché sur google etc. mais nada !

Merci d'avance.
-----

[GuYem]

Le théorème du rang est assez visuel :

Fais une patate pour représenter E. Dedans tu fais une patate pour représenter ker(f).
f mange tout ker(f) ( en ce sens qu'elle l'envoie sur le zero de F) mais elle ne mange pas ce qui reste dans E , qui est envoyé sur Im(f).

En résumé : dans E il y a ceux qui se font manger et ceux qui se ne se font pas manger...
Dim(E) = Dim(ker(f)) + Dim(Im(f))

[Draune]

Moi là je suis pas d'accord.
Premièrement il y a une ENORME faute dans l'énoncé du théorême du rang : il faut absoluement que E soit de dimension finie. Vous me direz que c'est sous-entendu quand on écrit dim(E) mais il faut quand même le mettre dans les hypothèses : tout simplement parce que sinon écrire dim(E) n'a pas de sens!!
Ensuite, à ce niveau (je pense que tu dois être au moins à bac +1 : soit en fac soit en prépa?), les maths deviennent vite trop abstraites pour qu'on puisse continuer à vouloir se représenter ce qu'on fait. Ici il faut apprendre à comprendre sans s'imaginer, ou alors à s'imaginer mais pas par rapport à des situations de la vie usuelle.
Et plus tu vas avancer dans tes études en maths, plus ça va devenir abstrait et imposoble à se représenter. Il faut s'y faire...
Draune

[martini_bird]

Et plus tu vas avancer dans tes études en maths, plus ça va devenir abstrait et imposoble à se représenter. Il faut s'y faire...

Heureusement que non. Il faut au contraire construire une image mentale de ce que l'on fait: l'abstraction sert à simplifier, non à compliquer.

De plus, dans les ev, il suffit de raisonner sur les vecteurs de la base: le théorème du rang dit que ce qu'il y a dans le noyau ne peut être réalisé dans l'image. Mais plus précisément, il dit qu'une application linéaire décompose (en somme directe) l'espace de départ en une partie projetée sur 0 (le noyau) et une partie isomorphe à l'image.

Cordialement.

[A voir en vidéo sur Futura]

[GuYem]

Moi là je suis pas d'accord.
Premièrement il y a une ENORME faute dans l'énoncé du théorême du rang : il faut absoluement que E soit de dimension finie. Vous me direz que c'est sous-entendu quand on écrit dim(E) mais il faut quand même le mettre dans les hypothèses : tout simplement parce que sinon écrire dim(E) n'a pas de sens!!
Ensuite, à ce niveau (je pense que tu dois être au moins à bac +1 : soit en fac soit en prépa?), les maths deviennent vite trop abstraites pour qu'on puisse continuer à vouloir se représenter ce qu'on fait. Ici il faut apprendre à comprendre sans s'imaginer, ou alors à s'imaginer mais pas par rapport à des situations de la vie usuelle.
Et plus tu vas avancer dans tes études en maths, plus ça va devenir abstrait et imposoble à se représenter. Il faut s'y faire...
Draune

Comme martini je ne suis pas trop d'accord avec ça.
Cependant chacun sa technique ; mais personnellement j'essaye toujours de me représenter par un moyen ou un autre ce sur quoi je suis en train de travailler. Ou au moins d'en avoir un exemple, au mois méga simple ; ca permet de se rendre compte des applications que peuvent avoir ce qu'on fait.
L'abstraction et la généralisation c'est sympa mais il faut quand même voir sur quoi on travaille

[justine&coria]

Moi là je suis pas d'accord.
Premièrement il y a une ENORME faute dans l'énoncé du théorême du rang : il faut absoluement que E soit de dimension finie. Vous me direz que c'est sous-entendu quand on écrit dim(E) mais il faut quand même le mettre dans les hypothèses : tout simplement parce que sinon écrire dim(E) n'a pas de sens!!
Ensuite, à ce niveau (je pense que tu dois être au moins à bac +1 : soit en fac soit en prépa?), les maths deviennent vite trop abstraites pour qu'on puisse continuer à vouloir se représenter ce qu'on fait. Ici il faut apprendre à comprendre sans s'imaginer, ou alors à s'imaginer mais pas par rapport à des situations de la vie usuelle.
Et plus tu vas avancer dans tes études en maths, plus ça va devenir abstrait et imposoble à se représenter. Il faut s'y faire...
Draune

Tout d'abord désolé d'avoir oublié le fait que E doit être de dimension finie. Je t'aurais bien dit qu'au final ça ne change rien puisqu'on parle de dim(E), mais c'est vrai que dans ma tête j'avais oublié cette hypothèse.
Et en ce qui concerne la représentation. Je ne parlais pas d'image de patate etc. (merci beaucoup à Guyem au passage), mais je veux essayer de me visualiser le pourquoi de la chose. Si on a une formule aussi simple, c'est sûrement qu'il y a quelque chose de sous-jacent, chose que je ne voyais pas.
En effet, grâce à Guyem, j'ai réalisé que lorsqu'on passe de E à Im(f)=f(E), on perd des dimensions, justement parce que les dimensions de Ker(f) s'annulent par f : l'image de Ker(f) étant l'élément neutre (dimension=0) de l'ensemble d'arrivée.
Le théorème du Rang est à présent plus clair dans ma tête.

Au vu de ce que tu dis, t'as sans aucun doute fait beaucoup plus de maths que moi, et il y aura sûrement des "lois" que je devrais apprendre sans me les représenter (comme par exemple se représenter 4 dimensions etc.).
Mais bon, je pense qu'il faut toujours essayer de se visualiser. Au moins faire des analogies, avoir en tête un exemple simple qui rende bien du théorème.

Ici par exemple, rien que le fait d'avoir pris mon temps à essayer de comprendre pourquoi le théorème du Rang est ainsi, fait que cette formule je la retrouverais très facilement dans le futur, contrairement à beaucoup d'autres. Et c'est à présent plus clair dans ma tête.

[martini_bird]

Comment je vois le théorème du rang: il existe un sev V de E tel que avec .

Et ceci vaut en dimension infinie.

[justine&coria]

Comment je vois le théorème du rang: il existe un sev V de E tel que avec .

Et ceci vaut en dimension infinie.

Ah ouais, c'est pas du tout con ça !!

Enfin, juste une question, pourquoi tu mets "" ? Ca veut dire "à peu près égal" ou ça a une signification que je ne connais pas (encore) ?

[GuYem]

Ca veut dire isomorphe ; ie il existe une isomorphisme linéaire (une application linéaire bijective) entre V et im(f), c'est exactement cet isomorphisme que l'on construit dans la preuve

[martini_bird]

Salut,

le signifie isomorphe à. En dimension finie, est équivalent au fait que dim E=dim F.

EDIT: grillé par Guyem

[justine&coria]

Merci beaucoup à vous 2 !
Sans avoir vraiment compris ce qu'est un isomorphisme, j'ai compris la proposition de Martini_Bird. C'est fort ça !!

[Quinto]

Le théorème du rang est encore vrai en dimension infinie...(A t'il un quelconque intéret cependant?)
Et dim(E) si E est de dimension infinie a un sens, c'est le cardinal d'une base (on peut montrer que c'est bien défini).
On peut même montrer que si Dim(E)=dim(F) alors F et E sont isomorphes (en fait on a l'équivalence...)
Je ne vois donc pas de problème là dedans...
A+

[bendesarts]

Bonjour,

j'aimerais reprendre cette discussion. Je suis également très interessé de comprendre ce théorème avec les mains mais je n'ai pas encore compris à l'aide des discussions précédentes... Il me semble que la linéarité de l'application n'a pas trop été évoquée alors que c'est elle qui doit permettre d'obtenir le théorème du rang.

"Dans les ev, il suffit de raisonner sur les vecteurs de la base: le théorème du rang dit que ce qu'il y a dans le noyau ne peut être réalisé dans l'image" --> OK, mais celà est une conséquence du théorème du rang mais ne me fais pas sentir pourquoi le théorème du rang est vrai.

"Mais plus précisément, il dit qu'une application linéaire décompose (en somme directe) l'espace de départ en une partie projetée sur 0 (le noyau) et une partie isomorphe à l'image" --> même remarque que précédement.

Avec "les mains", Est-ce que vous pourriez m'expliquer à partir du schéma ci-dessous le théorème du rang ?

J'aimerais notamment comprendre pourquoi à partir de ces deux seules hypothèses :
a) les ensembles de départ E et F sont des eVs
et
b) l'application f de E dans F est linéaire on arrive à démontrer que f est bijective et donc obtenir le théorème du rang ?

Schéma :


Merci d'avance pour votre aide.

[minushabens]

Je ne vois pas trop ce que tu veux dire par "avec les mains". Et je ne vois pas non plus ce que tu ne comprends pas. Peut-être pourras-tu te convaincre de la véracité de la relation en prenant quelques exemples d'endomorphismes de R^3 ? Il y a 4 possibilités pour la dimension du noyau...

[gg0]

Bendesarts,

Ton dessin ne rend pas vraiment compte de la situation, car il n'y a pas de raison pour que tous les éléments de F soient des images (il y a une partie de F qui est Im(E). Ton E n'est pas décomposé en somme directe de Ker(f) et une partie isomorphe à Im(f). Donc la flèche isolée ne représente rien. Enfin ton application f n'est pas définie, et à priori, n'est pas une bijection de E-ker(f) dans F (ni injective, ni surjective).

Le fond du problème est ceci :
Si deux éléments de E ont la même image, alors leur différence est dans ker(f) (conséquence de la linéarité). Ce qui fait qu'on peut choisir un supplémentaire de Ker(f) dans E, et que ce supplémentaire a la même dimension que Im (f). En fait, n'importe quel supplémentaire convient.

Il n'y aura pas de démonstration "avec les mains", ça n'existe d'ailleurs pas en maths (ne pas confondre démonstration et exemple), mais de ta part, si tu veux comprendre, un changement de représentation pour les espaces vectoriels (les patates n'intègrent pas la notion de dimension), par exemple une représentation par l'espace muni d'une origine (le 0 de l'EV), pour les sev, des plans ou droites passant par l'origine, et pour des sommes directes, le fait que l'intersection est réduite à l'origine. Puis un apprentissage très sérieux de toutes les propriétés de ton cours (toutes sont ou seront nécessaires) pour gagner de l'intuition sur les notions de dimension et de linéarité.

Bon travail !

[AncMath]

En fait le theorème du rang découle tres simplement d'un simple théorème de structure pour les applications linéaires tres facile à démontrer.

Pour toute application linéaire tu peux regarder le produit où est le noyau de l'application et un supplémentaire de celui ci.
L'application est alors égale à la composition . La première flèche est un isomorphisme et est simplement donnée par les projections d'un vecteur sur ses composantes selon et . La second flèche est la projection de sur . La troisième est simplement restreinte à et la dernière est l'inclusion de dans . Il est tautologique que restreinte à induit un isomorphisme de sur . Le vrai contenu du théorème du rang est alors que si est un isomorphisme alors ce qui n'est pas un théorème si trivial que ça.

Autrement dit toute application linéaire est la composé d'une projection suivie d'un isomorphisme suivi d'une inclusion. Et il est facile de comprendre comment chaque étape affecte la dimension. En fait il suffit de se rappeler que si l'on réécrit les choses en fonction de la projection alors cela devient ce qui est le théorème du rang pour une projection et duquel la formule générale découle.

Ceci n'a pas l'air totalement canonique et c'est vrai : il faudrait plutôt prendre pour le quotient mais si tu ne sais pas ce que c'est alors la présentation donnée est suffisante

[JB2017]

Bonjour
Voici ce que je lis. voir en particulier ce que j'ai mis en gras.
"
Avec "les mains", Est-ce que vous pourriez m'expliquer à partir du schéma ci-dessous le théorème du rang ?

J'aimerais notamment comprendre pourquoi à partir de ces deux seules hypothèses :
a) les ensembles de départ E et F sont des eVs
et
b) l'application f de E dans F est linéaire on arrive à démontrer que f est bijective et donc obtenir le théorème du rang ?
"


Il faut arrêter le massacre! Qui peut arriver à démontrer avec les mains cette énormité en gras. Les mathématiques c'est du sérieux.

[AncMath]

Il me semble que les messages qui suivent celui que tu cites dissipent cette "énormité".

Mais pour poursuivre ma réponse à bendesarts et notamment cette partie

Il me semble que la linéarité de l'application n'a pas trop été évoquée alors que c'est elle qui doit permettre d'obtenir le théorème du rang.

En fait la linéarité n'a que peu à jouer ici. L'idée fondamentale heuristique est plus générale et est celle ci : si est un morphisme entre objets géométriques et , alors pour un choix général de on devrait avoir . Cela est basée sur l'idée que l'on veut voir comme la famille des paramétrée par . Un sorte de "produit" donc et pour un produit les dimensions devraient s'ajouter.

Bien sur c'est totalement faux en général en plus d’être assez imprécis. Mais c'est une philosophie générale qui marche "souvent". Pour les espaces vectoriels elle marche toujours en prenant et en fait quitte à définir la dimension d'un translaté d'un sous-espace vectoriel comme la dimension du sous espace en question, cela marche pour n'importe quel . Bien sûr dans cette preuve la linéarité intervient, tu as raison.

D'ailleurs la preuve que j'ai donné plus haut réponse totalement sur le fait de voir à isomorphisme près comme le produit

J’espère que cela éclairera bendesarts sur pourquoi on s'attend à ce genre de théorème.