volume d un tore

[invite3c2a67c1]

Bonjour,
Je me demandais ,comment( d'une manière générale) avoie la certitude lors du calcul d'un volume
que le decoupage initial est correct?:
Par exemple je veux calculer le volume d 'un tore:
au depart je prends un cercle de surface pi.r*r (r :rayon interieur au disque resultant d'un plan
orthogonal coupant le tore et R voir fichier joint)
puis : somme de tous les disques multiplieé par delta angle du rayon "interieur (R-r)
je m aperçois que le resultat est faux.
Alors je "decoupe plus finement en disant V=V1+V2
V=Sc.da.(R-r) + Sc.[da.(R+r)-da.(R-r)]/2 (da:lire d alpha)
V=Sc.da(2R-2r+R+r-R+r)/2
V=Sc.da(2.R)/2=pi.r.r.da.R
da integrer de 0 a 2pi => V=pi.r.r.(2.pi).R=2.pi².r².R
MAIS SUR INTERNET ILS NE PROCEDENT PAS DU TOUT COMME CELA (le plan de decoupage
est different et ils font la difference de 2 VOLUMES
C'est pourquoi :existe il une methode qui nous indique "comment modeliser au depart" ?
car meme ici j ai l'impression de tomber au "hasard"
sur le volume correct
Merci par avance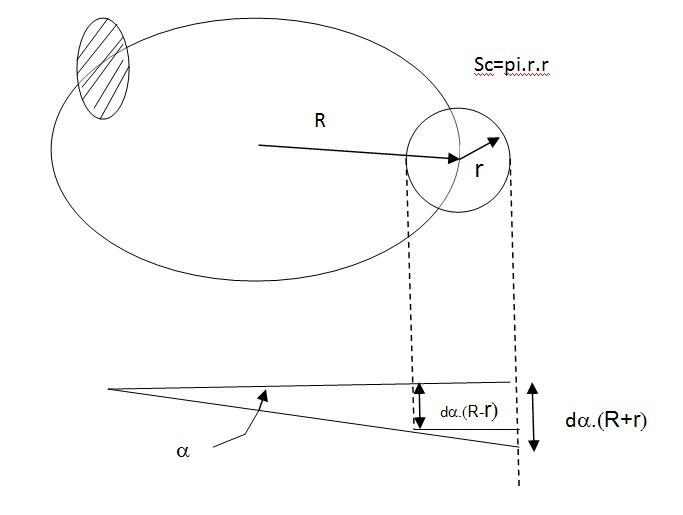
-----

[God's Breath]

MAIS SUR INTERNET ILS NE PROCEDENT PAS DU TOUT COMME CELA

Peux-tu donner la référence précise afin que l'on puisse comprendre ?

[invite3c2a67c1]

Par exemple sur
http://www.sciences.ch/htmlfr/geomet...ieformes01.php
ou
http://www.matheureka.net/Q12.htm

[God's Breath]

Effectivement, la découpe sur les liens que tu présentes est pratique, mais pas forcément naturelle.
De plus, il faut être capable de justifier la formule :



pour le calcul du volume d'un solide de révolution.

Pour ta méthode, dans l'angle , tu as une tranche du tore qui est une sorte de cylindre.
Cette tranche a une épaisseur «intérieure» de , une épaisseur «extérieure» de , et une épaisseur «médiane», au niveau du centre du cercle Sc de surface , de .
On assimile donc cette tranche à un cylindre droit de base le cercle Sc et de hauteur l'épaisseur «médiane», en considérant que ce qui manque du côté intérieur est compensé par ce qui dépasse du côté extérieur.
Vue ainsi, la tranche du tore a pour volume : et, en intégrant :

[A voir en vidéo sur Futura]

[invite3c2a67c1]

Merci bien,mais même comme cela existe il une méthode "infaillible" ,par exemple
avec les équation d un plan coupant le volume ,ou encadrant le volume par 2 autre volumes
min et max avec une limite vers zéro (un peut comme lorsque l on encadre une suite numérique)
ou doit on raisonner avec un "découpage" arbitraire qui risque d'aboutir à un faux resultat
sans possibilité de vérifier?