Bonjour voilà j'ai un problème avec un exercice avec lequel je sais pas trop comment m'y prendre. J'ai peur de mal procéder. Voici l'exo :
Soit fi € R.
(1) Dessiner sur un sch00ema les nombres complexes, 1, exp (i fi), et 1 + exp (i fi).
(2) Écrire le nombre complexe z = 1 + exp (i fi) sous forme trigonométrique (on pourra s'inspirer du schéma de la question (1)).
(3) En déduire une expression simple de (1 + cos fi + i sin fi)n, pour tout n € N*.
Merci de votre aide.
-----




 peut être représenter dans un repère orthonormé
peut être représenter dans un repère orthonormé  ...
...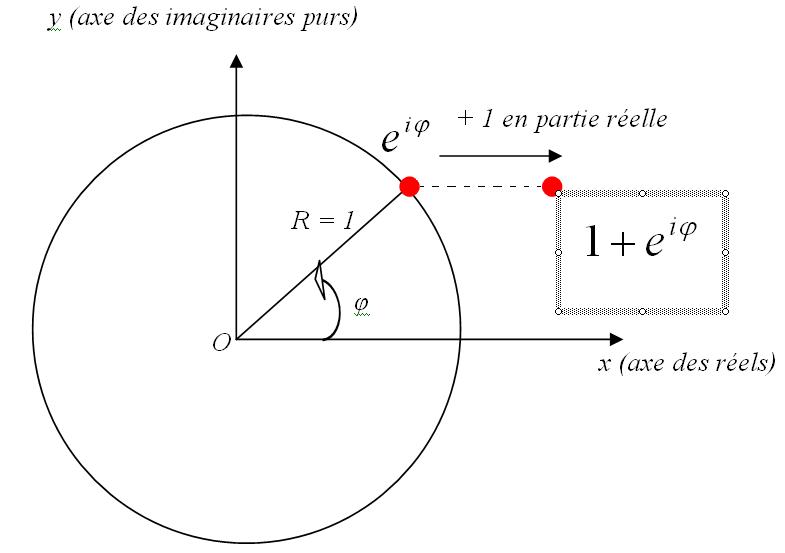
 Logique puisque tu ne rajoutes pas de partie imaginaire mais que tu fais une simple translation selon l'axe
Logique puisque tu ne rajoutes pas de partie imaginaire mais que tu fais une simple translation selon l'axe