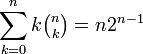Preuve par induction

[inviteb0350bdd]

Je dois prouver par induction que la Sommation de j=0 jusqu'à n pour j(j dans n)est égale à n2^(n-1)

J'avoue que je suis un peut bloquée. J'ai commencé par prouver que c'est vrai pour n=1. Puis j'ai supposé que c'était vrai pour n=k.

Je voudrais maintenant le prouver vrai pour n = k+1 mais je suis bloquée.

Merci!

Désolée, je ne comprend pas comment écrire pour que vous puissiez voir les symboles.

À noter que j dans n, je veux dire combinaison de j dans n
-----

[invite57a1e779]

Je traduis :

Tu considères la somme , tu veux prouver que :

Tu as commencé par prouver que c'est vrai pour .

Puis tu supposé que c'était vrai pour , et tu voudrais passer à .

Tu supposes connaître la valeur de , et tu veux calculer la valeur de : il va falloir utiliser, pour la relation du triangle de Pascal : , ainsi que : et .

Cela te permettra d'exprimer en fonction de .

[inviteb0350bdd]

Voilà j'ai trouvé

[inviteb0350bdd]

J'avais trouvé comment l'écrire mais merci Je vais essayer ce que tu viens de me dire et je t'en redonnes des nouvelles!

[A voir en vidéo sur Futura]

[inviteb0350bdd]

Ok j'ai trouvé la valeur pour j=0 et ça m'a donné 0, donc je vais commencer ma sommation à j=1

Mais en développant j , je suis arrivée à la même chose que k* . Donc, vu que k est une constante, j'ai pu la sortir de ma sommation, et j'en suis arrivée à dire k *

Et c'est à partir de là que je suis un peu mélangée. Je me suis dis que je pouvais remplacer par - et que de là je pouvais séparer mes sommations et arriver à
k* 2^k - 2^k-1

Mais je vois bien que ce n'est pas égal à (k+1)2^(k+1)-1

....................

[invite3240c37d]

Sans induction c'est plus simple :

[inviteb0350bdd]

Je suis bien d'accord, mais je dois vraiment le prouver par induction :S

Mais merci