Bonjour à tous, je me permets de vous poser une question qui est une suite logique de la précédente avec une fonction similaire à un point prêt.
Soit une fonction f avec x définit sur [0,+infini], défini sur R par f(x) = [(x)²]/[racine(1+Cx²+x³)]=[(x)²]/[(1+Cx²+x³)^(1/2)]
1) Calculer sa dérivée , f'(x) et annuler là.
Mon problème est que je suis bloqué pour la dérivée la fonction f(x) malgré toutes vos explications à la précédente question à cause de la racine carrée:
je procède comme suit:
u(x)=[(x)²] et v(x)=[(1+Cx²+x³)^(1/2)]
(u(x)')=2*x et (v(x)')=[2*C*x+3*x²]/[2*((1+Cx²+x³)^(1/2))]
d'où j'utilise f'(x)= [(u(x)')*v(x) - u(x) * (v(x)')]
et je trouve :
puis je suis bloqué car je ne sais pas comme m'arranger avec la racine carrée à la fraction du numérateur...
-----




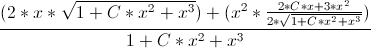
 qui s'écrit
qui s'écrit 

