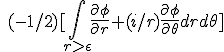dérivée partielle de 1/z par rapport à z(barre) comme distribution

[invite4ef47b18]

Bonjour tout le monde

J'ai montré dans un exercice que la dérivée partielle par rapport à z(barre) de (1/z) est une fonction holomorphe sur C privé de 0.
et j'ai besoin de calculer la valeur de cette distribution appliquée à une fonction test phi (ça doit donner pi* Dirac).

Je calcule donc l'intégrale en utilisant la définition de l'opérateur de Cauchy Riemann et le passage aux coordonnées polaires (je calcule l'intégrale sur {r>epsilon} pour faire tendre epsilon vers 0 par la suite).

Je trouve donc comme expression:



Mais là je bloque, je ne vois pas ce que je pourrais faire!

Merci d'avance pour votre aide.
-----

[deyni]

Bonjour,

juste pour si retrouver:

Vous cherchez à calculer:

[invite4ef47b18]

non, en fait je cherche à calculer la dérivée de 1/z par rapport à zbarre appliquée à phi!

[albanxiii]

Bonjour,

Et la définition générale (à adapter au cas ) : n'est pas valide ici ?

Bonne soirée.

[A voir en vidéo sur Futura]

[invite76543456789]

Salut!
Comme hier, il te suffit d'utiliser la formule de Stokes.
Ca te donne , en developpant les deux cotés tu obtiens ton résultat.

[invite4ef47b18]

Salut

Je ne vois pas vraiment ce que vient faire le log ici! mais en tout cas c'est vrai que je dois utiliser la formule de stockes (Green Riemann) à ce stade.



mais je ne vois pas comment je pourrais faire apparaître le phi de 0!

[invite76543456789]

Ben le d(log'(z)) te donne un dz/z, et ensuite tu as a calculer l"intégrale sur le cercle de rayon espilon de i.phi(z), ce qui tend vers 2i.\pi.phi(0) le membre de droite lui donne l'intégrale que tu dois calculer.

[invite4ef47b18]

Là j'applique la formule de Green Riemann, ce qui me donne ca



C'est une intégrale curviligne à calculer pour ensuite faire tendre epsilon vers 0 et tomber sur pi*dirac

Le paramétrage à utiliser ici est: r(t)=epsilon et thêta quelconque, mais je ne vois pas vraiment comment l'utiliser pour calculer cette intégrale curviligne!

[invite76543456789]

La premiere intégrale est nulle (dr est nulle quand tu la restreint au cercle) la deuxieme intégrale se calcule facilement en soustrayant par exemple 2\pi\psilon \phi(0)... sinon tu peux aussi lire ce que j'ai ecrit et qui te donne directement la réponse (et qui est le meme calcul).

[invite4ef47b18]

Pour la deuxième intégrale ca donne (-1/2)*phi(0)*2pi = -pi*phi(0) c'est bon, sauf qu'il y a un problème avec le moins!
Pour ce que tu a écrit, ca donne: l'intégrale sur {r=epsilon} de phi(z)/z dz à gauche, et le terme à droite est le terme recherché.
Le terme de gauche doit donc tendre vers pi*phi(0) mais comment ca ?

[invite76543456789]

Le moins ne viendrait il pas du fait que l'a oublié quand tu as fait passer la dérivée à droite dans le crochet?
Pour calculer et bien c'est exactement la meme chose que ton calcul, car ca vaut tu soustrait 2i\pi phi(0) et tu montre que la difference tend vers 0.

[invite4ef47b18]

Non, je n'ai pas oublié le moins quand j'ai fait passer la dérivée à droite dans le crochet. Je crois que si j'intègre sur le cercle de rayon epsilon il faut encore préciser le sens dans lequel on parcourt le cercle pour avoir ou bien l'intégrale de 0 à 2pi ou bien de 2pi à 0 d(thêta). Seulement, je ne sais pas comment on précise ce sens !

[invite76543456789]

L'orientation sur le bord est l'orientation exterieure dans la formule de stokes (autrement dit l'orientation induite).

[invite4ef47b18]

Mon domaine ici est R2 privé du disque de rayon epsilon. Le bord de ce domaine est le cercle de rayon epsilon, je dois le parcourir de sorte que mon domaine soit à gauche, c'est donc le sens trigonométrique, c'est à dire de 0 à 2pi. Or ça doit être le contraire!

[invite76543456789]

Ben il y a une erreur de calcul, reprend le depuis le debut, tu devrais trouver, la méthode est la bonne.