problème de géométrie

[invite84e89f3d]

Bonjour à tous,

J'ai actuellement un problème de géométrie, je n'arrive pas à trouver les angles qu'il me faut et même si j'ai l'impression que la solution est toute bête je n'arrive pas à la trouver alors j'espère que vous pourrez m'aider. pour ceux qui auraient vu, j'ai posé le même problème dans la section lycée, mais je me dis que peut être c'était dans cette section que je devais le mettre



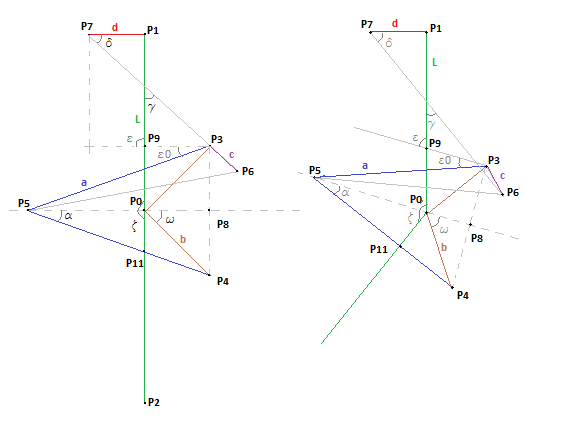
Voici la géométrie, les longueurs et angles fixes sont les suivant :
L = P0P1 = P0P2
a = P5P3 = P5P4
b = P0P4 = P0P3
c = P3P6
d = P1P7
l'angle epsilon0 = angle(P5P3P9) qui est défini pour dzeta = 180° , donc pour dzeta < 180° on aura toujours epsilon0(dzeta<180°) = epsilon0(dzeta=180°)
l'angle (P5P3P6) qui est défini pour dzeta = 180°, idem que pour epsilon0, on a angle(P5P3P6)(dzeta<180°) = angle(P5P3P6)(dzeta = 180°)
Et on connait aussi l'angle dzeta

Ce que l'on cherche c'est à déterminer tous les autres angles, alpha, omega, epsilon, gamma et delta en fonction des données si dessus.

On sait que :
[P5P0] est la bissectrice de l'angle 2*alpha
[P5P0] est la bissectrice de l'angle dzeta
[P5P0] est la bissectrice de l'angle 2*omega
angle(P0P8P3) = 90°
lorsque dzeta = 180° on a epsilon = 90° et omega = 45°
[P7P6] est confondu avec [P7P3] et [P3P6] lorsque dzeta = 180° mais ce n'est plus le cas lorsque dzeta < 180°


Voici les relations que j'ai déjà trouvé :

sin(omega) = (P4P8)/b ] donc sin(omega) = a*sin(alpha)/b
sin(alpha) = (P4P8)/a ]

sin(epsilon0)=(P3P8)/a = (P4P8)/a = sin(alpha) = b*sin(omega)/a
Comme epsilon0 est fixe, on peut directement le calculer en considérant omega = 45°.
Donc epsilon0 = arcsin(b*sin(45°)/a)

sin(gamma) = (d+(P3P9))/(P7P3) = (d+b*cos(omega))/(P7P3)
En utilisant le théorème de Pythagore dans le triangle P7P3P12 (P12 étant le point à l'intersection des trais en pointillés partant de P7 et P3)
On obtient P7P3² = P1P9² + P12P3²
avec P1P9 = L - b*sin(omega) et P12P3 = d +b*cos(omega)
Donc on obtient :
P7P3 = rac( (L-b*sin(omega))² + (d+ b*cos(omega))²)

d'où gamma = arcsin((d+b*cos(omega))/rac( (L-b*sin(omega))² + (d+ b*cos(omega))²))

Pour delta c'est très simple : car angle(P7P1P9) = 90°
delta = 90° - gamma

Puis angle(P5P3P6) = 180°-delta -epsilon0
On peut faire directement le calcul car nous savons que omega = 45° et que angle(P5P3P6) est un angle fixe


Au final j'arrive à avoir tous mes angles en fonctions de omega ....

Il me manque plus que omega en fonction de dzeta.
Si quelqu'un peut m'aider à trouver omega en fonction de dzeta je lui en serais très reconnaissante.

si vous souhaitez d'autres explications ou d'autres données qui vous manqueraient pour y arriver, n'hésitez pas à me demander.

Merci d'avance de l'aide que vous pourrez m'apporter.

Le but de cet exercice est de pouvoir reconstituer toute la figure pour chaque dzeta donné. Il me faut donc les coordonnées de chaque point en considérant que P0 est le centre du repère et que nous avons un repère orthonormé direct. Cela me permettra au final de programmer le système en Matlab pour qu'en donnant dzeta j'ai directement la géométrie correct.

Fonia
-----

[ericcc]

Si je lis bien ton diagramme, tu as une espèce de flèche qui tourne autour d'un point P0.

Ta flèche est symétrique par rapport à l'axe P5/P8.

Dans ces conditions l'angle n'a aucune raison de dépendre de ta variable

En fait il est évident de voir que

[invite84e89f3d]

Bonjour,

lorsque je construit la figure avec seulement l'angle dzeta de connu, je peux construire l'angle alpha et l'angle omega en faisant de cette manière :

_ je trace l'angle dzeta ,
_ je trace la bissectrice de l'angle dzeta,
_ je place le point P5 sur la bissectrice en considérant la longueur P0P5 identique à la longueur P0P5 lorsque dzeta = 180°
_ en utilisant un compas, je trace le cercle de centre P5 et de rayon a
_ en utilisant un cmpas, je trace le cercle de centre P0 et de rayon b
_ les points d'intersections entre les deux cercles sont les points P3 et P4
_ je trace ensuite les segments P5P3 et P5P4 ainsi que P0P3 et P0P4
_ j'obtiens donc la "flèche" et je peux définir l'angle omega = angle entre P0P4 et la bissectrice et l'angle alpha = angle entre P5P4 et la bissectrice.

En faisant de cette manière j'ai donc obtenu mes angles alpha et omega alors qu'au début je n'avais que l'angle dzeta, je pense donc effectivement qu'il y a une relation entre dzeta et alpha ou entre dzeta et omega (puisque omega et alpha sont liés cela n'a pas vraiment d'importance).

J'avais effectivement trouvé la relation entre omega et alpha (qui est en rouge dans mon premier post).

Si vous avez d'autres questions, n'hésitez pas à me les poser, j'essaye toujours de mon côté de trouver la relation qui me manque.

Fonia

[mécano41]

Bonjour à tous,

...
_ je place le point P5 sur la bissectrice en considérant la longueur P0P5 identique à la longueur P0P5 lorsque dzeta = 180°
_ en utilisant un compas, je trace le cercle de centre P5 et de rayon a
_ en utilisant un compas, je trace le cercle de centre P0 et de rayon b
...

Ces trois lignes confirment ce que t'a dit Ericcc : Le triangle P0P5P3 garde ses trois côtés constants et connus pendant la rotation donc oméga est constant...

Il doit y avoir une erreur dans ton explication.

A mon avis, il faudrait déjà mettre dans un repère XPoY les points qui ne se déplacent jamais (P7, P1...)et dans un repère UPoV les points qui seront fixes dans ce dernier repère (P5, P3, P4...). Ce repère est confondu avec XPoY si dzeta = 180° et il tourne en Po de dzeta-180° (donc sens négatif pour respecter ta figure)...

Cordialement

[A voir en vidéo sur Futura]

[invite84e89f3d]

Bonjour à tous,

j'ai finalement réussi à trouver ce que je voulais, je m'excuse pour ericcc car effectivement j'ai trouvé que omega et alpha ne dépendait pas de dzeta mais seulement des longeurs a, b et P0P5.

Donc en utilisant le théorème de pythagore généralisé j'obtiens :
b² = a² + P0P5² -2*a*P0P5*cos(alpha) donc alpha = arcos((a²+ P0P5² - b²)/(2*a*P0P5))

Ce qui fait que mon sytème "tourne' au final c'est l'angle entre la bissectrice et l'horizontal (appelé angle de deflection) qui se calcul de cette manière :
angle de deflection = 1/2*angle entre la verticale et L2
angle de deflection = 1/2*(180-dzeta)

Donc voilà, j'ai réussi à faire mon système.

Si vous avez des questions sur ce que j'ai fait, demandez.

Fonia