DL a l'ordre 2

[invite4c80defd]

bonjour a tous , voila , j'ai un probleme avec plusieurs exos
Le premier est d'écrire un Dl en 0 a l'ordre 2 de f(x)=(x+1)/(x-2)
mais je n'arrive pas a transformer l'expression pour utiliser les Dl usuels
merci d'avance
-----

[Médiat]

Bonjour,

En remarquant que (x+1)/(x-2) = (x - 2 + 3)/(x-2) vous devriez vous en sortir.

[invite4c80defd]

ah oui , merci j'avais pas remarquer cela
Pour 1/sqrt(4-x^2)
j'ai dit que cela revenait a dire : (sqrt(4-x^2))^0.5 mais apres il faudrait simplifier ce 4-x^2 mais comment ?
merci d'avance

[gg0]

Bonjour.

Si c'était 1 à la place de 4, on pourrait utiliser le DL de (1+x)^alpha. Donc on s'y ramène en factorisant le 4 sous la racine on obtient où t tend vers 0 quand x tend vers 0.

Cordialement.

[A voir en vidéo sur Futura]

[invite4c80defd]

en effet , ça fonctionne , merci pour l'astuce

[invite4c80defd]

Merci pour ces réponses.
j'ai encore besoin de vous pour cet exo: c'est ok pour la 1 et la 2 mais je bloque a la 3
merci pour votre aide

[gg0]

Appliquer la question 2.

[inviteaf1870ed]

La 1 aussi pour le a)

[invite4c80defd]

Bonjour et merci d'avoir répondu.
je vais vous communiquer dans les plus brefs délais ce que j'ai fais pour que l'on puisse avancer sur le probleme

[invite4c80defd]

voici donc ce que j'ai fais, et ds pour la clarté de la photo

[inviteaf1870ed]

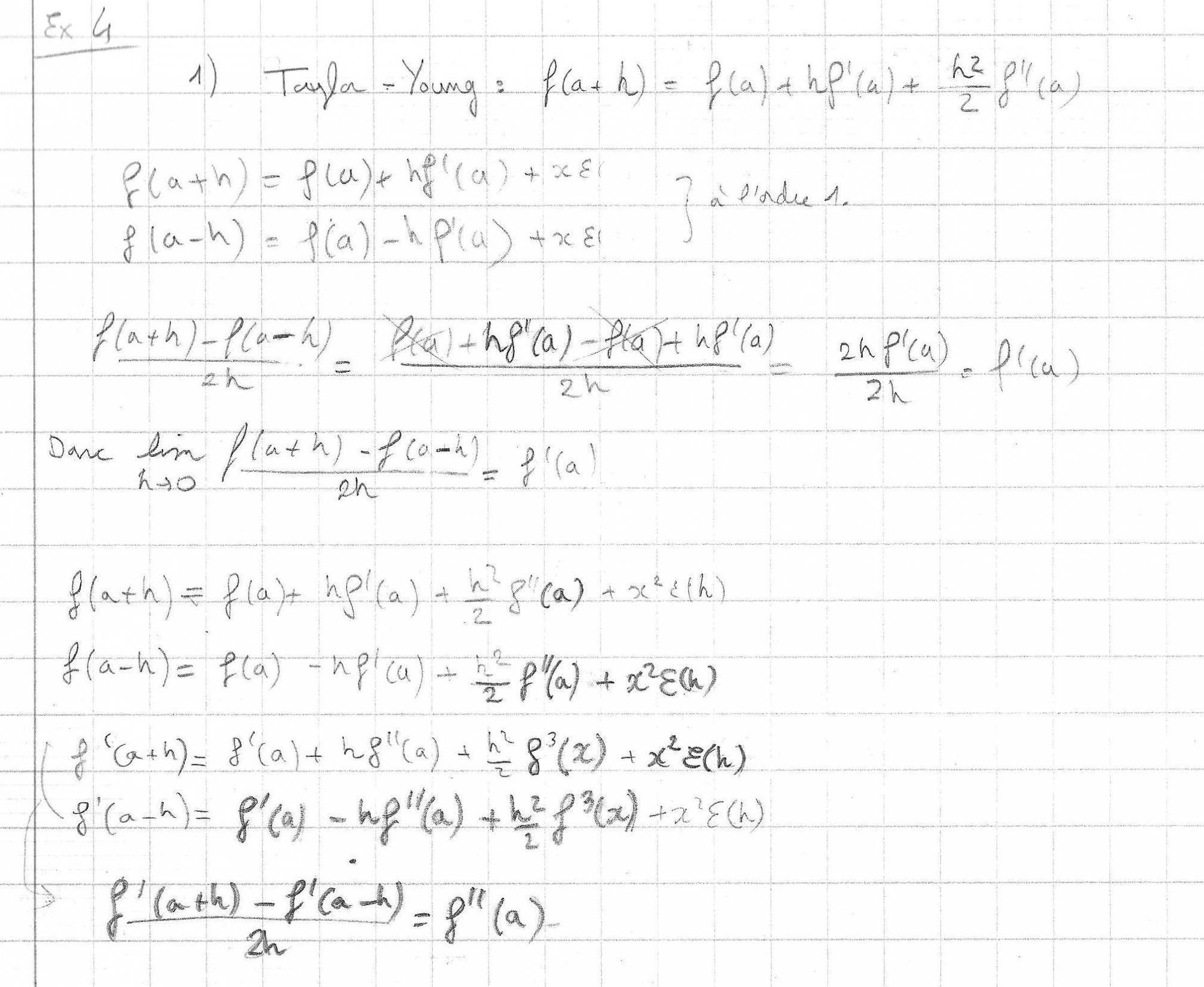
Bah tu ne réponds pas à la question que l'on te pose avec ton deuxième calcul...

[gg0]

Attention,

tu sembles simplifier les qui n'ont rien à voir les uns avec les autres, puisque ce sont des calculs différents. Il serait plus sain alors de noter pour f(a+h) et pour f(a-h). Idem pour la suite.
Résultat, tes calculs sont en partie faux ! f'(a) ne se calcule pas en fonction de f(a+h), f(a-h) et h..

Cordialement.

[invite4c80defd]

d'accord, merci pour ces réponses
Il me faut donc modifier mes x*E(x) pour bien les distinguer.
sinon , pour mon expression de f''(a), c'est bon ? mis a part mes x*E(x)

[gg0]

Ben...

comme ce que tu as écrit est faux, difficile de dire "c'est bon".

[invite4c80defd]

d'accord, c'est vrai je me suis mal exprimé, je voulais demander si ma démarche et mes enchainements de calculs étaient corrects ?

[gg0]

Si tu les corriges, je pourrai savoir. La justesse des calculs fait partie de la démarche.

[invite4c80defd]

j'ai retravaillé cet exercice et j'étais visiblement fatigué le jour où j'ai commencé...bref, j'ai trouvé la solution a mon probleme qui était en fait , tout bete.
je vous remercie pour vos réponses qui m'on mis sur la piste et vous souhaites une bonne soirée.