trajets d'une particule

[kaderben]

Bonjour
Voici un exo dont j’ai essayé de faire les deux premières questions et la troisième sera pour plus tard.



1°) Pour chaque déplacement il y a 4 possibilités (i,j,-i,-j) donc d’après le principe multiplicatif, le nombre total de trajets est :4*4*4*4 = 256 trajest possibles
2°)
a) Vect(OA) = 2i + 2j, 2 déplacements selon i et 2 déplacements selon j
Je les ai comptés et même j’ai fait un arbre et je trouve 6 trajets
Je me demande s’il n’y a pas une autre méthode pour calculer le nombre de trajets car si par exemple on avait A(8 ;10) et bien c’est quasiment impossible de compter ou faire un arbre.
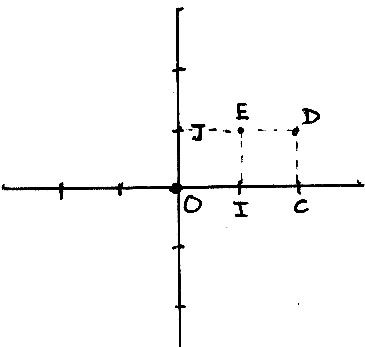
b) Soit M(x,y) ou’ la particule arrive puis retourne au point O.
Vect(OM + MO) = xi+yj-xi-yj
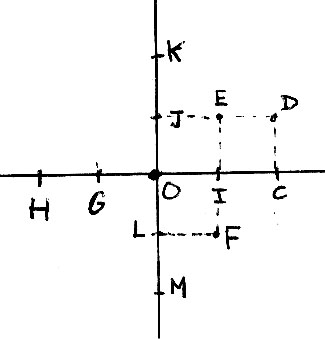
x=0 alors y=2 d’ou Vect(OM + MO) = 2j-2j 2 points M1(0;2), M2(0;-2) qui fait 2 trajets
x=1 alors y=1 d’ou Vect(OM + MO) = i+j-i-j 8 points 8[(1;1), (1;-1), (-1;1), (-1;-1)] qui fait 8 trajets
x=2 alors y=0 d’ou Vect(OM + MO) = 2i -2i 2 points (2 ;0), (-2 ;0) qui fait 2 trajets
donc 12 trajets en tout.
Là aussi, y’a t il pas plus simple ?

Merci pour vos commentaires
-----

[RoBeRTo-BeNDeR]

Bonjour, pour la 2 oui il y a plus simple, en gros tu dois faire deux fois HAUT et deux fois DROITE. Au lieu de compter les trajets, tu aurais pu te demander comment placer tes deux HAUT parmi les quatre déplacements, les droite complétant ainsi les 2 coups restants. Il y a 2 parmi 4 possibilités, donc 6 si je ne m'abuse.

Pour la 2)b), logiquement, il doit y avoir autant de HAUT que de BAS, de DROITE que de GAUCHE.

Après disjonction des cas. Je pense que ça ressemble beaucoup à ce que tu as fait.


RoBeRTo

[Tryss]

Attention, pour la b), il y a plus de 12 trajets.

En partant dans une direction fixée au premier coup (par exemple à droite) :

Il y a 2 trajets qui "bouclent" (par exemple : droite, haut, gauche, bas)
Il y a 4 trajets qui repassent par O (par exemple : droite, gauche, bas, haut)
Il y a 3 trajets qui ne repassent pas par O et qui ne bouclent pas (par exemple : droite, droite, gauche, gauche)

Et par symétrie, il y en a 4 fois plus de trajets si on considère les 4 directions pour le premier coup (qui donnent des trajets différents)

Soit 9*4 = 36 trajets possibles pour revenir en O.

[Tryss]

Le temps étant écoulé pour éditer le message précédent, je double post

Pour prendre le problème de façon plus générale, on peut tout d'abord fixer le nombre de fois ou on va a droite (ça fixe le nombre de fois ou on prend chaque direction), puis ensuite arranger ces directions :

Si on va 0 fois à droite, on va 2 fois en haut et 2 fois en bas, et il y a donc C(2,4) trajets de cette façon (on choisi les 2 emplacements des déplacements hauts)
Si on va 1 fois à droite, on va 1 fois dans chaque direction, et il y a donc 4! trajets de cette façon
Si on va 2 fois à droite, on va 2 fois à gauche, et il y a donc C(2,4) trajets de cette façon

Et on retrouve les 36 trajets.

On peut étendre ce type de raisonnement a un nombre pair quelconque de déplacements.

Par exemple, pour 10 déplacements :

0 fois à droite, donc C(5,10) déplacements
1 fois à droite, donc C(1,10)*C(1,9)*C(4,8) déplacements
2 fois à droite, donc C(2,10)*C(2,8)*C(3,6) déplacements
3 fois à droite, donc C(3,10)*C(3,7)*C(2,4) déplacements
4 fois à droite, donc C(5,10) déplacements

On remarque d'ailleurs que le nombre de trajets ou l'on va k fois à droite lors d'un trajet de longueur 2n qui fini en 0 est le même que celui ou on va n-k fois à droite (en effet, on va alors k fois à gauche, et par permutation ce résultat est logique)

[A voir en vidéo sur Futura]

[kaderben]

Bonjour
Vous trouvez 36 trajets pour la quedtion 2°) b)
Ci dessus un dessin ou' j'ai compté que 12 trajets



Dans le premier quadrant:
OICIO, OIEJO, OJEIO donc 3 trajets et par symétrie: 3*4 = 12 trajets

[Tryss]

Sauf que tu en oublie plein : par exemple "droite, bas, haut, gauche" ou encore "droite, gauche, gauche, droite"

Et tu ne les obtiens pas par symétrie, puisque le premier mouvement ne serra pas droite par symétrie

[kaderben]

Effectivement, j'ai mal compté !
Je vais refaire les comptes.
Merci pour la remarque.

[Amanuensis]

Annullé....

[Amanuensis]

Par exemple, pour 10 déplacements :

0 fois à droite, donc C(5,10) déplacements
1 fois à droite, donc C(1,10)*C(1,9)*C(4,8) déplacements
2 fois à droite, donc C(2,10)*C(2,8)*C(3,6) déplacements
3 fois à droite, donc C(3,10)*C(3,7)*C(2,4) déplacements
4 fois à droite, donc C(5,10) déplacements

Y'a pas une typo ? La dernière ligne à remplacer comme suit ?

4 fois à droite, donc C(4,10)*C(4,6)*C(1,2) déplacements
5 fois à droite, donc C(5,10) déplacements

[Amanuensis]

On remarque d'ailleurs que le nombre de trajets ou l'on va k fois à droite lors d'un trajet de longueur 2n qui fini en 0 est le même que celui ou on va n-k fois à droite (en effet, on va alors k fois à gauche, et par permutation ce résultat est logique)

Et ça ça me perturbe. Ce ne serait pas plutôt "(en effet, on va alors k fois vers le haut, et par permutation ce résultat est logique)" ?

[Amanuensis]

L'égalité se retrouve formellement en réalisant que le nombre est le coefficient multinomial C(2n, [k, k, n-k, n-k]), ce qu'on peut rationaliser a posteriori...

[Fin de mes commentaires un peu HS...]

[Tryss]

Oui Amanuensis, tes remarques sont justes. Je vais (sournoisement) attribuer ces erreurs à l'heure d'écriture du message

[kaderben]

Bonjour
Voilà, j'ai recompté, effectivement j'ai oublié 8 trajets:



Selon i on a: OIFIO, OIEIO donc 2 trajets
Selon -i,j,-j la même chose
donc selon i,-i,j,-j on a 8 trajets
Ce que j'ai compté avant je le rappelle ici:
Dans le premier quadrant:
OICIO, OIEJO, OJEIO donc 3 trajets et par symétrie: 3*4 = 12 trajets

En tout je compte 12 + 8 = 20 trajets

Est ce que je me trompe, je n'en sais rien, mais 36 trajets me paraissent beaucoup

Merci

[Amanuensis]

Si vous prenez les trajets combinant les 4 mouvements différents, vous en avez 4!, soit 24 à eux tous seuls.

Les 12 autres sont les allers-retours linéaires, DGDG, DGGD, DDGG, fois 4 .

[Amanuensis]

HS, ou plutôt ES (extension de sujet) :

Les premières valeurs sont 4, 36, 400 et 4900. Que des carrés, et la suite des racines est 2, 6, 20, 70, où l'on reconnaît les C(2n,n). Conjecture : le nombre de possibilités pour 2n mouvements est (C(2n,n))². Démonstration ???

[Amanuensis]

Suite ES : Je crois avoir trouvé !

Au lieu de prendre les déplacements (0,1), (0, -1), (1, 0) et (-1, 0), on fait un changement de repère pour travailler avec (-1, -1), (1, -1), (-1, 1) et (1, 1). On a alors découplé les deux dimensions, et suffit de répartir n + et n - sur l'une, C(2n, n) cas, et de même sur l'autre. Total (C(2n,n))² cas. Application numérique n=2, (6!)² = 36.

[kaderben]

Je n'en suis pas encore là :
"Les premières valeurs sont 4, 36, 400 et 4900. Que des carrés, et la suite des racines est 2, 6, 20, 70, où l'on reconnaît les C(2n,n). Conjecture : le nombre de possibilités pour 2n mouvements est (C(2n,n))². Démonstration ??? "

Les trajets que tu cites:
"Les 12 autres sont les allers-retours linéaires, DGDG, DGGD, DDGG, fois 4 . "

ce ne sont pas des trajets sur le dessin que j'ai fait , à moins que, je sais pas quoi.
Merci

[Amanuensis]

Les trajets que tu cites:
"Les 12 autres sont les allers-retours linéaires, DGDG, DGGD, DDGG, fois 4 . "

ce ne sont pas des trajets sur le dessin que j'ai fait , à moins que, je sais pas quoi.

En quoi posent-ils un problème ? Ces trajets sont parmi ceux indiqués par Tryss. J'ai juste répété un peu différemment son décompte :

Si on va 2 fois à droite, on va 2 fois à gauche, et il y a donc C(2,4) trajets de cette façon

C(2,4) (en utilisant sa notation), c'est 6, cela correspond à DGDG, DGGD, DDGG, et les trois autres obtenus en permutant G et D.

Où est le problème ?

[kaderben]

Je crois qu'il y a un malentendu, c'est pour ça je n'ai pas compris les trajetsGDG, DGGD, DDGG
Tu veux dire à partir de O: on se déplace à droite (i) puis à gauche (-i) puis à droite (i) puis à gauche (-i) ce qui nous donne pour le premier selon mon dessin:
OIOIO qui repasse deux fois par O
Je croyais qu'on considère que les trajets qui reviennent une seule fois en O pour finir, comme par exemple: OIEJO
Peut être j'ai mal interprété la question.
Merci pour tout.

[Amanuensis]

Je croyais qu'on considère que les trajets qui reviennent une seule fois en O pour finir

Cela change évidemment le décompte !

Cependant j'ai beau lire et relire l'énoncé, message #1, et je n'y trouve rien qui indique une telle limitation.

[Amanuensis]

PS : Le nombre de parcours passant par l'origine au bout du deuxième mouvement est 4x4=16 (4 possibilités pour le premier couple, 4 pour le second), il en reste bien 36-16=20 ne passant pas au centre avant la fin, comme vous avez compté.

[kaderben]

ça fait plaisir que tu confirmes les 20 trajets que j'ai compté, car comme je ne suis pas trop rapide, j'ai mis du temps!

Je n'ai pas encore regardé la théorie dans vos messages mais je vais m'y mettre et ensuite je passerai à la troisième et dernière question qui est apparemment pas facile.
Merci pour tout.

[Amanuensis]

Je n'avais pas encore lu la troisième question ; il me semble qu'elle confirme l'analyse selon laquelle il faut compter, question 2, les trajets passant par O deux fois...