Cosinus épousant une courbe

[deshonest]

Bonjour,

J'espère que vous allez bien et que l'été se passe bien ! Je suis confronté à un problème (qui n'est pas un exo, ni DM ou DS mais une problématique à laquelle je suis confronté dans une étude de design mécanique):

Tout comme une courbe y=h.cos(b.x) (h et b étant param..) peut être tracée sur une droite
Capture d’écran 2013-07-15 à 11.17.37.png

Il est relativement aisé de "tracer" un cosinus pour qu'il épouse la courbure d'un cercle:
x= r+h.cos(r.tetha.b)
y= r+h.sin(r.tetha.b)

Capture d’écran 2013-07-08 à 16.25.39.png

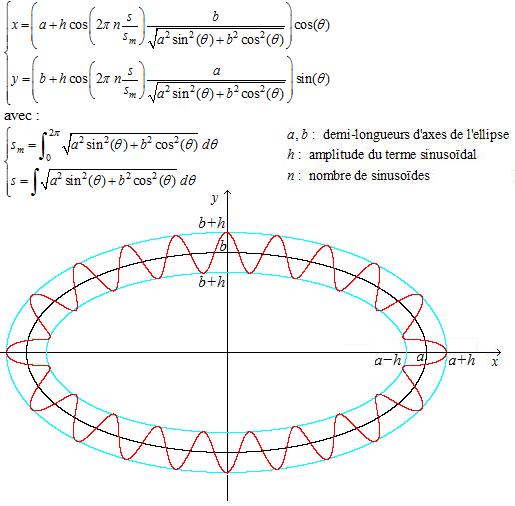
Il devient plus difficile de faire ça pour une courbe quelconque, ici pour une ellipse par exemple :
Capture d’écran 2013-07-15 à 11.21.44.png

A première vu tout a l'air ok, mais sur les cotés de l'ellipse où la courbure est importante la période de l'éllipse n'est pas la même...

L'idée ce serait donc de connaitre en coordonnées polaire la longueur de l'arc d'une fonction quelconque en fonction de tetha. Ou alors d'approximer les arcs de la courbe par des cercles et de tracer consécutivement le cosinus... Des suggestions ? des Idées ? Je suis un peu confus a vrai dire...

Merci par avance !

Umar
-----

[invite06622527]

Bonjour,

Si j'ai bien compris ce que tu souhaites, il faut porter le terme sinusoïdal sur le vecteur normal à l'ellipse et l'argument du terme sinusoïdal doit être proportionnel à la distance parcourue sur l'ellipse.
Les formules données en page jointes satisfont ces conditions. La variable "s" est la distance parcourue sur l'ellipse(dont le périmètre est noté "sm").
Le calcul de s se fait aisément par intégration numérique, à mesure que l'on incrémente theta, lorsqu'on trace la coube point par point (exemple sur la page jointe). Une autre manière de faire consisterait à utiliser une fonction elliptique de seconde espèce si elle est implémentée dans le logiciel.

Désolé, actuellement l'envoi de document joint ne marche pas. Il ne s'agit pourtant pas d'un gros fichier : JPG (40ko, 515x506 pixels). J'essaierai à nouveau de l'envoyer un peu plus tard.

[invite06622527]

Page jointe :

[Dlzlogic]

Bonjour,
De mémoire, l'abscisse curviligne sur une ellipse est difficile, voire impossible, à calculer. Par contre, son approximation à une parabole donne de très bons résultats.
A vue de nez, la sinusoïde semble légèrement déformée sur le cercle. Est-ce une illusion d'optique ou pas ?

[A voir en vidéo sur Futura]

[invite06622527]

Note : pour une écriture plus correcte, sur la figure remplacer "nombre de sinusoïdes" par "nombre de périodes sur un tour complet"

[invite06622527]

Bonjour,
De mémoire, l'abscisse curviligne sur une ellipse est difficile, voire impossible, à calculer. Par contre, son approximation à une parabole donne de très bons résultats.
A vue de nez, la sinusoïde semble légèrement déformée sur le cercle. Est-ce une illusion d'optique ou pas ?

C'est vrai : la longueur parcourue sur l'ellipse ne peut pas s'exprimer avec un nombre fini de fonctions usuelles. C'est la raison pour laquelle l'intégration numérique est ce qu'il y a de plus simple dans le cas présent. Mais elle peut s'exprimer formellement grâce à une fonction spéciale (Fonction elliptique de seconde espèce). Mais encore faut-il que cette fonction soit implémentée dans le logiciel de tracé de courbe que l'on utilise.
Il est également vrai que la "sinusoïde" (qui n'en est plus une si on parle de façon rigoureuse) apparait déformée et elle est effectivement déformée. Il ne peut pas en être autrement : imaginez une "vraie" sinusoïde tracée sur une bande plane de caoutchouc. Déformez cette bande de façon à ce qu'elle soit courbe (tout en restant plane). Les sommets supérieurs de la sinusoïde s'écartent les uns des autres alors que les sommets inférieurs se rapprochent les uns des autres. C'est bien ce que l'on observe sur la figure.