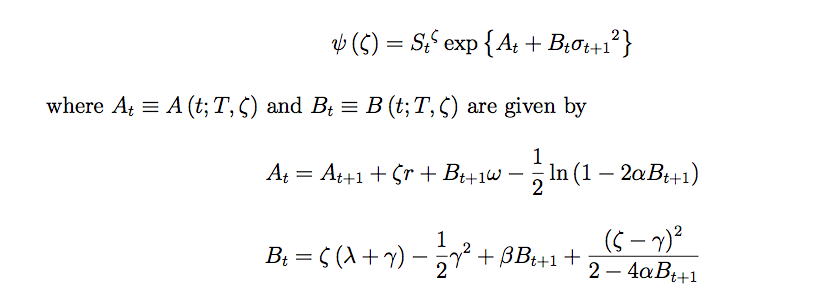Transformée de Fourier et inversion de fonction caractéristique

[invitebfb0bb71]

Bonjour, je travail sur un article et je n'ai pas assez de connaissance sur l'inversion des fonctions caractéristiques. Ce n'est pas des mathématiques pures mais peut-être pourriez-vous m'aider.

En fait je suis sur un processus qui suit un GARCH et les auteurs déterminent une fonction génératrice qui à cette forme :
Capture d’écran 2013-09-30 à 17.09.57.png

Qu'ils réécrivent sous la forme :

Capture d’écran 2013-09-30 à 17.02.46.png

avec :

Capture d’écran 2013-09-30 à 17.05.47.png

Il montrent qu'avec un GARC(1,1) il est possible de travailler par récursion avec les conditions terminales suivantes :

Capture d’écran 2013-09-30 à 17.06.36.png

Jusque là je comprend plus ou moins même si la démonstration est tendu, en gros j'arrive à comprendre.

Donc ils nous disent que pour passer à la fonction caractéristique il suffit de remplacer par jusque là je comprend (plus ou moins).

Il utilisent la méthodologie de Feller (1971) et Kendal et Stuart (1974) pour inverser la fonction caractéristique et obtienne ça :

Capture d’écran 2013-09-30 à 17.12.13.png

Alors là je suis dans la galère, je comprend même pas la démonstration qu'ils font : tout est dispo ici :http://bfi.cl/papers/Heston%20Nandi%...on%20model.pdf

Je croyais que pour inverser une fonction caractéristique on devait avoir recours à la transformé de Fourrier, j'ai du mal à comprendre ça je l'ai jamais vu en cours j'ai regardé sur wikipedia, mais pour inverser il faut pas que la fonction caractéristique soit une transformé de fourier ? donc il faudrait déjà le montrer ? Merci pour votre aide
-----

[invitebfb0bb71]

Edit en fait je pense c'est plus facile en bossant sur un GARCH(1,1)



Vous savez pourquoi il faut déterminer A et B de façon récursive ?
Après j'imagine que ça doit être plus simple pour déterminer l'inverse de cette fonction caractéristique que dans la forme que j'ai donnée précédemment. Mais je vois pas comment faire