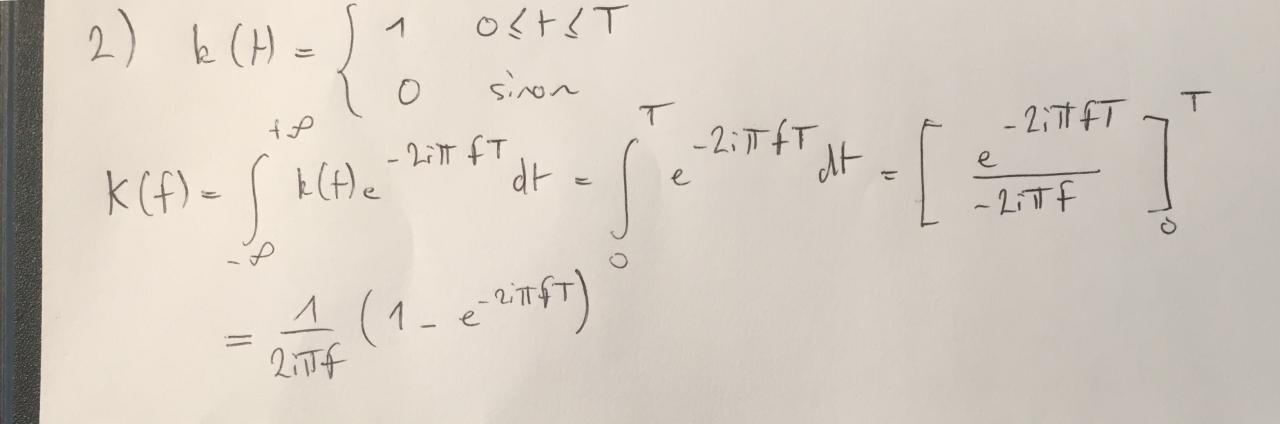Transformée de Fourier de la fonction porte

[invite2c91a2eb]

Ma fonction est défini de manière à ce que entre 0 et T elle vaut A et partout ailleurs elle vaut 0.
Je n'arrive pas à trouver sa TF où plutôt j'arrive à un résultat différent que lorsque elle est centré en 0 ( entre -T/2 et +T/2 ).
Normalement je devrais trouver ATsinc(pi*f*T) et moi j'ai ATsinc(2pi*f*T)

Merci d'avance de m'aiguiller car j'ai du faire une erreur idiote et pas moyen de la retrouver.
-----

[invite3240c37d]

Par rapport à la porte centrée, ta fonction subit une translation de T/2, donc sa transformée de Fourier subit une multiplication par ..

[invite8f5247dd]

Bonjour,

Je déterre ce vieux sujet car j’ai quelques questions pour un calcul identique.
Lorsque je déroule le calcul je ne vois pas comment faire apparaître un sinus cardinal à la fin puisque j’ai un 1 au numérateur. Il faudrait faire apparaître un exp(2i pi f T ) mais je ne vois pas comment...pourtant cette fonction étant juste une porte translatee de T/2 on devrait pouvoir faire apparaître un sinus cardinal ?
Voici mon calcul :

[albanxiii]

Bonjour,

Factorisez par . Comme votre porte n'est pas centrée sur zéro, c'est normal qu'il y ait un terme de phase non nulle avec le sinus cardinal (propriété de translation des transformées de Fourier).

EDIT : d'ailleurs, cf message #2

[A voir en vidéo sur Futura]

[invite8f5247dd]

En effet j’avais bien trouvé ce résultat mais je cherchais le résultat du post #1, or il y manque le terme en exponentielle, et je me suis acharné à vouloir le faire disparaître, donc on a bien Tsinc(πfT)exp(-iπfT).
Merci albanxiii

[gg0]

Comme quoi, il faut lire aussi les réponses à la question? Mmu disait déjà ce que t'a répondu Albanxiii.

Cordialement.