Bonjour
J'ai un problème pour trouver le domaine de définition de cette fonction.
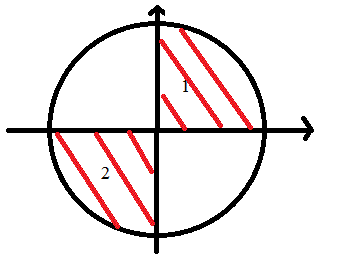
Je sais que les fonctions sinus et cosinus sont des fonctions trigonométriques et je me demandais si dire sin(x)cos(x)≥0 aiderais a déduire que le domaine est {Df=1U2} avec ce schémas
Ou je suis a côté de la plaque ?
Cordialement.
-----