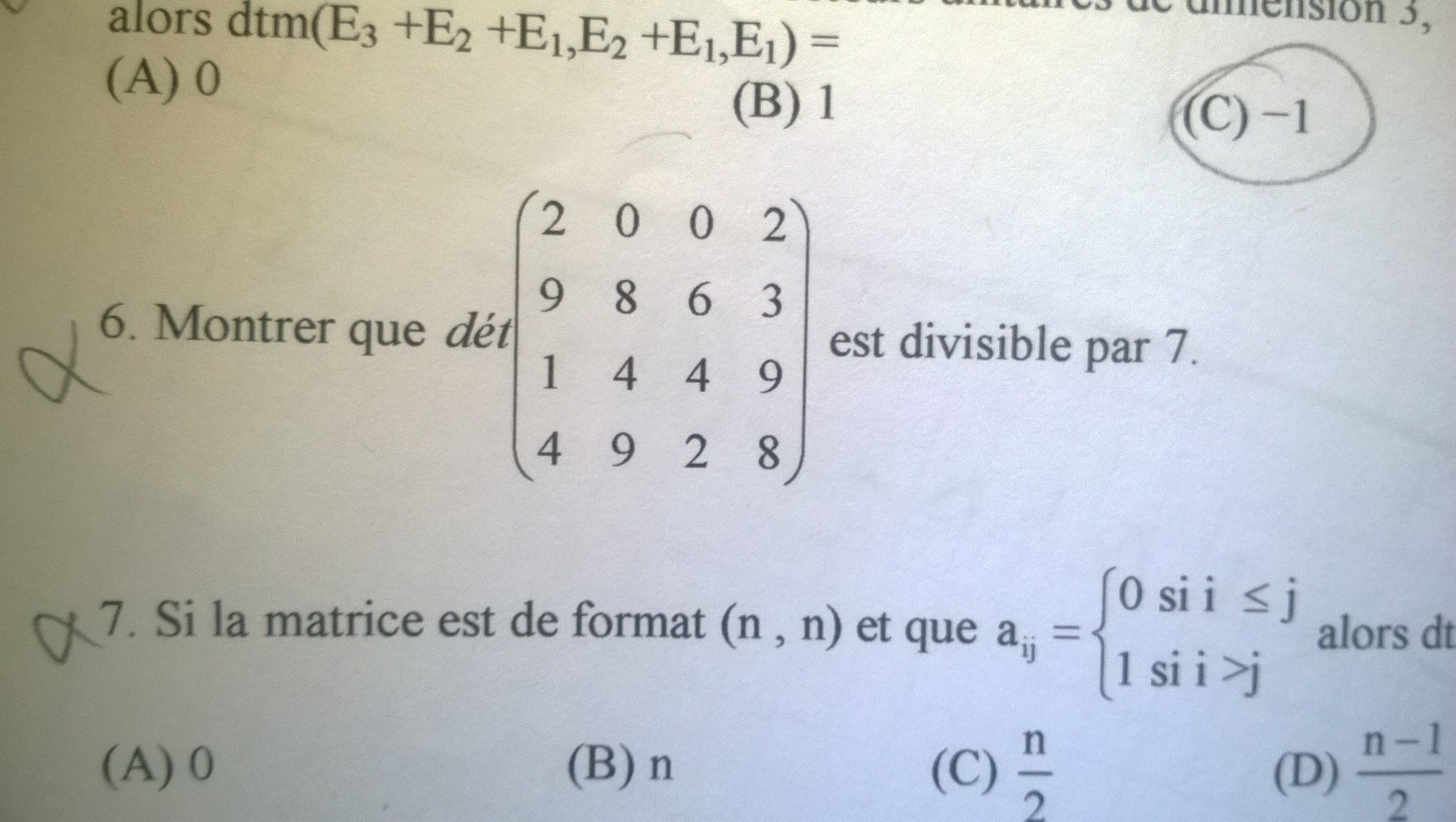Calcul du déterminant par la méthode des mineurs et des cofacteurs

[invitec6a48323]

Bonjour à tous, je me tourne à nouveau vers vous pour m'aider à élucider un mystère mathématique .

En effet, je travaille actuellement, comme le mentionne l'intitulé de ce message, sur le calcul du déterminant par la méthode des mineurs et des cofacteurs (sans passer par la méthode de Sarrus pour les matrices d'ordre 3).

Voici l'énoncé (question 6) :

J'ai fait plusieurs fois ce calcul et figurez-vous que en fonction des opérations sur les lignes et colonnes que j'ai faites, la valeur du déterminant à la fin différait. La première fois il était bien divisible par 7. La seconde fois, non.

Je sais également qu'il ya un moyen plus rapide pour trouver la réponse (simplement en faisant L3-2.L4, donc en soustrayant la 3eme ligne par le double de la 4eme ligne) mais ce n'est pas ce problème que je veux souligner.

En fait, faut-il faire les opérations sur les lignes et colonnes comme on veut ou faut-il, par exemple, ne soustraire que les lignes par une autre ligne ayant un nombre plus grand ? Genre est-ce que la ligne 1 ne peut qu'être soustraite et ne jamais soustraire ? Je m'explique : L1 peut être soustraite par L2, L3, L4 et L2 peut-être soustraite que par L3, L4, etc. ?

Car il s'avère que lorsque je travaille dans mon cours et que je ne suis pas les mêmes opérations que celles du professeur puisque je fais les opérations qui instinctivement m'apparaissent, je n'arrive pas à un déterminant qui a la même valeur.

En espérant avoir été clair et dans l'attente de vos réponses,

Louis.Gr
-----

[invitec6a48323]

Voici un exemple qui pourrait peut-être mieux illustré mon problème :

Voici l'énoncé : WP_20140807_005.jpg

La résolution avec le prof : WP_20140807_002.jpg

La réponse est 36

Ma résolution : WP_20140807_004.jpg

La réponse est 21

Pourtant, lorsqu'on regarde la résolution du professeur, on remarque que systématiquement c'est une colonne "supérieure" soustraite par une "inférieure" du type C4-2.C3 etc. alors que dans ma résolution, ya aussi C4-2.C3 et à un autre moment intervient l'opération dans l'autre sens du type C1-2.C2 .

Est-ce c'est pour cela ? Il ya-t-il une méthode "systématique" à adopter lors de l'utilisation de la méthode des mineurs et des cofacteurs ?

Bien à vous

[gg0]

Bonjour.

Il semble (j'ai du mal à lire) qu'il y a une erreur de calcul dans tes modifications de lignes. Je n'ai d’ailleurs pas réussi à lire quels changements tu fais, tu écris trop petit et mal.

Cordialement.

[invitec6a48323]

Désolé, je ne m'attendais pas à être lu au moment où j'écrivais.. Ceci dit, il est possible d'agrandir l'image en double cliquant dessus. J'ai pourtant vérifier à plusieurs reprises si il ne s'agissait pas d'une bête erreur de calcul avant de poster ceci sur le forum dans la crainte de mettre des choses inutiles en ligne. D'autant plus que ceci se répète à chaque élucidation de déterminant quand je ne suis pas la même démarche que le professeur, je ne pense donc pas que l'erreur vient simplement d'une opération entre lignes ou colonnes...

[A voir en vidéo sur Futura]

[gg0]

Tu pourrais au moins dire ce qui est écrit, c'est ta question !
Quand c'est mal écrit, même grossi, c'est illisible.

L'ordre des lignes ou des colonnes n'a pas d'importance dans la modification (voir ton cours). La principale erreur qu'on peut faire, c'est en modifiant plusieurs lignes à la fois de "tourner en rond". mais si tu appliques bien la règle du cours, tu arrives au résultat.

Finalement, en reprenant ton déterminant 3x3 et le comparant à celui du prof, je vois que tu as simplement mal copié le dernier nombre !!!

[invitec6a48323]

Ah, effectivement, je viens de notifier que la feuille faite avec le professeur est erronée. J'ai perdu un (-1) dans la mêlée et 3*13 ne fait pas 36 mais 39 donc -39 serait la réponse. Ensuite, concernant le 21 trouvé par moi-même, j'ai omis de mettre un "-" devant le 3 en dernière position !

Merci en tout cas pour votre éveil, je vous suis très reconnaissant !