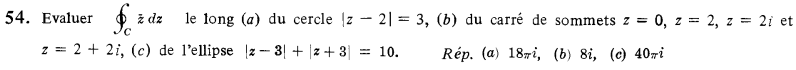Formule d'élipse

[topmath]

Bonjour à tous :

Voilà je patine sur cette exercice non pas sur ça solution , je veux dire je coince sur la formule d’ellipse à partir des complexe !!


Car c'est la première fois que je vois une formule d'ellipse donnée sous forme de complexe et valeur absolue , le reste je mon charge pour le calcule intégrale .
Si quelqu'un peut m'aider ou m'expliquer comment à partir de on arrive à en coordonnés cartésien encore faut il trouver après transformation et merci d'avance (c'est la question c qui m'intéresse ).

Amicalement
-----

[phys4]

Bonjour,
Si vous voulez retrouver la forme simple en x,y. Vous remplacez les modules de z-3 et z+3 par leurs valeurs.

Comme la formule signifie simplement que la somme des distances aux points -3 et +3 est une constante, il est évident qu'il faut trouver une ellipse dont les foyers sont connus. Mais suivant les questions posées, il n'est sans doute pas nécessaire de reconstituer l'équation cartésienne.

Bonne chance

[topmath]

Bonjour :

Merci d'abord phys4 pour la réponse , mais je ne parvient toujours pas à la comprendre cette notation , mais pour le calcule intégrale je veux justement évitez la forme complexe de la formule de Green en la transformant en une intégrale double pour cette raison l’utiliser des coordonner cartésien est commode je pense !!

Cordialement

[gg0]

Bonjour Topmath.

Tu as donc l'ensemble
Comme |z-3| est (cours classique) la distance entre M et le point A d'abscisse 3, et |z+3|=|z-(-3)| est la distance entre M et le point B d'abscisse -3, c'est donc l'ensemble des points M tels que MA+MB=10, ce qui est l'équation d'une ellipse de centre le milieu de [AB], c'est à dire l'origine O du plan; les axes sont donc (AB)=(Ox) et (Oy); le demi grand axe est 5 (les points de coordonnées (-5,0) et (5,0) sont les extrémités du grand axe), le demi-petit axe est 4 (par application du théorème de Pythagore, on voit que les points de coordonnées (0,-4) et (0,4) sont sur le petit axe); donc une équation est

Tout ceci est une application directe des cours classiques sur l'ellipse, comme on le faisait autrefois en terminale en France.

Maintenant, comment obtenir directement l'équation à partir de |z-3|+|z+3|=10 ? Bêtement, en posant z=x+iy puis en transformant pour faire disparaître les racines carrées. Amuse-toi bien !

Cordialement.

NB : Ta pièce jointe ne m'est pas encore visible.

[A voir en vidéo sur Futura]

[topmath]

Bonjour à tous :

Effectivement gg0 c'est grâce à vous que je peut maintenant continuer le périple merci encore .

Amicalement


Nb:C'est très bien expliquer.