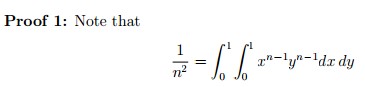Fonction zêta de Riemann, comment prouver ce résultat

[red17]

Bonsoir,

J'aimerai savoir comment faire pour démontrer le plus simplement possible ce résultat sachant que je passe en deuxième année de prépa en maths spé :


J'ai vu sur le net un fichier pdf de 14 preuves, mais je ne comprend pas vraiment le raisonnement de ces démonstrations.
C'est pourquoi, j'aimerai savoir s'il est possible que vous m'en donniez une, de sorte que je puisse la comprendre.

J'ai aussi une avec un polynôme en cotangente, mais je vois pas pourquoi on fait appel à cette fonction pour prouver ce résultat... etc.

Cordialement.

Merci d'avance !
-----

[invite90034748]

Si je me souviens bien tu peux intégrer la fonction 1/(1-xy) sur [0,1]x[0,1] de deux manière différentes : d'abord en voyant que c'est une série géométrique, ensuite par un changement de variables.

[red17]

J'aimerai savoir en particulier d'où sort cette égalité :


On a pas trop manipuler les intégrales doubles, du coup je vois pas d'où elle sort :/

Merci d'avance

[invite52487760]

Salut :
Quant une fonction à deux variables : est séparable, c'est à dire : quant : , alors, on a toujours : , puis, le reste du calcul n'est que le produit de deux simples intégrales à une seule variable qu'on calcule comme d'habitude.

[A voir en vidéo sur Futura]

[Zetalouest]

L analyse de Fourier est super pour ce genre de formule, après c est question de la ou vous êtes à l aise. Pour ce résultat on a la chance de la diversité des approches. Ce n est que zêta(2), en poussant un peu vous verrez que tous les zêta(2k) sont à deux pi près rationels. J ai cité cette formule il y a qq temps sur ce forum, pour souligner ce lien surprenant entre pi, zêta et les nombres entiers qui n à rien d intuitif. En tout cas en général.

[Zetalouest]

Enfin pour être précis je vous recommande https://www.google.fr/url?sa=t&sourc...GRaoA7dMQaw1KA attention Colmez est très synthétique, une approche sans solide base mathématiques peut être troublante

[red17]

Merci beaucoup pour le lien que vous avez recommandé.
Mais avant tout, voici un pdf que j'ai trouvé sur le sujet :
http://empslocal.ex.ac.uk/people/sta.../etc/zeta2.pdf

La preuve n°1 est une des preuves que j'aimerai connaitre, et maitriser.
C'est pourquoi j'aimerai savoir d'où sort l'affirmation :


Merci d'avance !

[invite90034748]

Fubini et le tour est joué. Note que (1/n)x^n est une primitive de x^{n-1} (et pareil pour y).

[red17]

Excellent, merci. J'en apprend plus
Je compte cette semaine proposer deux tentatives de preuves.

A bientôt