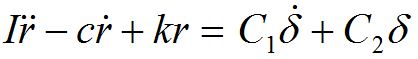Transformée de Laplace

[Zagstars]

Bonjour,

J'ai besoin de conseils afin de résoudre une équation différentielle.
J'ai un modèle qui réagit suivant cette équation :

I, c, k, C1 et C2 sont des coefficients.
r est l'output (domaine temporel).
Delta est l'input (domaine temporel).

Actuellement, j'ai la solution mais seulement pour une entrée de type saut indicielle. Mon but est de pouvoir y appliquer une entrée quelconque (ex: avoir une fonction de transfert et y appliquer l'entrée désirée). J'aimerais savoir comment résoudre cette équation via la transformée de Laplace (avec l'aide de Matlab si nécessaire ). J'ai quelques bases concernant les transformées de Laplace mais, pas suffisamment que pour résoudre une telle équation.
Vos conseils me seraient très utiles.

Merci et bonne journée.
-----

[stefjm]

Bonjour,
Une dérivée temporelle correspond à une multiplication par p dans le domaine transformée (condition initiale nulle).
D'où la fonction de transfert.
Cordialement.

[Zagstars]

Merci pour la réponse.

Donc si r(0)= et delta(0)=0, alors, la fonction de transfert est:
S(s)/E(s) = (C1*s + C2) / (I*s² - c*s + k)

Est-ce bien correcte ?

[CM63]

Bonjour,

Ben oui, ça me paraît simple, la fonction de transfert est une fraction rationnelle en p, et alors? Où est la difficulté? Oups je regarde ton message

A plus

[A voir en vidéo sur Futura]

[CM63]

Bonkour,

Merci pour la réponse.

Donc si r(0)= et delta(0)=0, alors, la fonction de transfert est:
S(s)/E(s) = (C1*s + C2) / (I*s² - c*s + k)

Est-ce bien correcte ?

Oui ça me paraît bon.