convergence simple et uniforme

[Confidential]

Bonjour!



pour la convergence simple

si x=0 On a fn(x) = 0
et si x>0 on a fn(x) = 1

donc fn(x) converge simplement

et on a pas la convergence uniforme

a ce que c juste ??
-----

[Confidential]

pardon c f(x) = 0 si x=0
et f(x)=1 si x >0

juste?

[gg0]

Bonjour.

Très bizarre ce que tu écris. Je suppose que ta notation f_n(x) signifie
Par contre, je ne saisis pas trop ce qu'est ce f(x). Si c'est la somme de la série, alors il serait bon d'étudier si ta série converge simplement. En utilisant les règles de convergence des séries simples. En tout cas, autant il est vrai que pour x=0, la série est la série nulle, donc vaut 0, autant pour x>0, il n'y a aucune conclusion évidente pour la somme.
Je ne sais d'ailleurs pas trop d'où tu sors ce 1.

Donc travail à recommencer, en appliquant posément des règles mathématiques (celles de ton cours).

Bon travail !

[Confidential]

parceque x est fixé . si pour ca j'ai fait f(x)=1 quand x prend la valeur 1 .

alors on a 3 cas f(x)=0 si ( x=0 ) , f(x)=1 si (x=1) , et f(x)=x ( x>0 et différent de 1 )

c'est ca monsieur??

[A voir en vidéo sur Futura]

[gg0]

Désolé, je ne comprends rien à ce que tu racontes.

Si tu as un cours sur le sujet (convergence de suites, convergence de séries) tu l'apprends pour savoir de quoi parle ton exercice. Si tu n'en as pas, tu en cherches un.
Mais pour l'instant, tu es à côté de la plaque.

Tu n'as pas répondu à mon interrogation : C'est quoi, f(x) ???

NB : pas de "monsieur" ici, je ne suis pas ton prof.

[Confidential]

d'accord je suis désolé .

voila la question



C'est ma faute oui, c'est une série c'est pas une suite ou une fonction ..

[Confidential]

par exemple x appartient à [0,+oo[

si x = 0
fn(x)=0

xi x>0 fixé
lim fn(x)=1

f(x) = 0 si x =0
f(x)=1 si x >0

fn converge simplement vers f(x)

[Confidential]

mais si on a :
x appartient à R
pour la convergence simple on fixe x .

si x = 0 , fn(x)=0

et pour les x différent de zéro ya rien ?

[gg0]

Pour les x non nuls, il faut étudier la convergence. Fais-le !

Nb : Pour l'instant, je ne peux pas lire la pièce jointe.

[Confidential]

si x = 1
on a la limite de fn(x) = 1

si x différent de 1 et 0 on a
la limitte fn(x) = 1/x

??

[gg0]

x=1 n'est pas un cas particulier. 1/x vaut 1 quand x=1. Plus gênant, c'est faux, la limite du terme général n'est pas 1/x !! Fais le calcul sérieusement.

Bon, j'ai compris de que tu voulais dire. Quelle idée de parler de f(x) ici !

Maintenant, il va peut-être falloir t'y mettre. Conformément aux règles du forum (http://forums.futura-sciences.com/ma...ces-forum.html), on peut t'aider, mais on ne fera pas ton travail à ta place.
D'autant qu'ici, la réponse est évidente si tu connais ton cours !!!

[Confidential]

#7 c'est un exemple d cours

alors j'ai fait les mémes étapes pour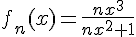

[gg0]

Ok, je ne comprenais pas, parce que ça n'a rien à voir avec ta question.

Bon, inutile de continuer tant que tu n'auras pas fait ton travail d'apprentissage. Tu n'es même pas capable de faire la différence entre convergence d'une suite (ton exemple de cours) et convergence d'une série (ton exercice). Il faut que tu arrêtes de copier sans comprendre, ça ne sert à rien.

Prends une bonne vingtaine d'heures pour revoir et comprendre les cours sur les suites et séries numériques, puis les cours sur les suites de fonctions, puis les séries de fonctions. Il te faudra bien ça pour comprendre. Après, tu reprendras ton exercice et tu verras qu'il est élémentaire.

Désolé !