2 façons de faire et pas le même résultat...

[invite9c7554e3]

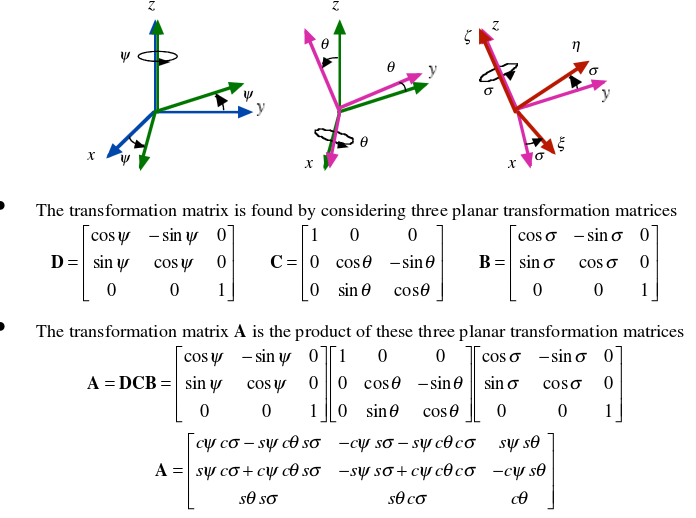
Bonsoir tous,

je fais 2 rotations (autour de z) et ensuite (autour du nouvel axe x nommé x') et je m'intéresse à la rotation globale qui me permet d'obtenir les nouvelles coordonnées en fonction des anciennes .

Avant de commencer, juste pour être certain que l'on est bien d'accord (?) quelques rappels :

• Matrice de transformation des vecteurs de base :

• Matrice de passage "P" (qui permet d'exprimer les nouvelles coordonnées en fonction des anciennes) sont les transposées des matrices et :

et

Calcul n°1 : les résultats me paraissent indiscutables car je retrouve des formules de mes cours de mécanique
on a et
soit au final

Calcul n°2 : je ne comprends pas pourquoi je ne retrouve pas le résultat ci-dessus
Soit un vecteur exprimé dans la base de départ :

et le vecteur exprimé dans la base qui a tourné également :

Si je remplace par
alors on trouve :

et si j'exprimer dans la base intiale :

alors je trouve (ce qui est égale à P1*P2:


Conclusion
- La logique voudrais que ma matrice de passage de x'' vers x soit et mon calcul 1 me permet de retrouver ceci
- Quand je fais le calcul détaillé je trouve par contre qui est faux mais j'ai refais les calculs et je ne vois pas d'erreur ?

Pourriez vous m'expliquez svp pourquoi ces différences ?
Merci énormément
-----

[Amanuensis]

Bonsoir tous,

je fais 2 rotations (autour de z) et ensuite (autour du nouvel axe x nommé x') et je m'intéresse à la rotation globale qui me permet d'obtenir les nouvelles coordonnées en fonction des anciennes .

Avant de commencer, juste pour être certain que l'on est bien d'accord (?) quelques rappels :

• Matrice de transformation des vecteurs de base :

La première matrice est celle d'une rotation autour de l'axe des x, pas de l'axe des x', non?

[Amanuensis]

PS: Suffit de prendre l'exemple de R1 envoyant x sur y, on a alors x'=y, y'=-x . R2 est une rotation autour de x', i.e., autour de y ; la matrice R2 doit donc laisser invariant y, et non x comme indiqué. Non?

[invite9c7554e3]

Tout d'abord merci beaucoup de prendre le temps de me répondre car ce problème me tracasse vraiment, ça me paraît très simple mais je n'arrive pas à retrouver le même résultat

La matrice R1 est celle qui permet de passer de à

R2 permet de passer de à

Voici un exemple de lien où on peut trouver ces relations (sauf que l'auteur donne les matrices de passage et pas celle de transformation des axes):
http://ressources.univ-lemans.fr/Acc...ngleeuler.html

[A voir en vidéo sur Futura]

[invite9c7554e3]

PS: Suffit de prendre l'exemple de R1 envoyant x sur y, on a alors x'=y, y'=-x . R2 est une rotation autour de x', i.e., autour de y ; la matrice R2 doit donc laisser invariant y, et non x comme indiqué. Non?

c'est bien l'axe e1' qui doit etre invariant :
http://www.u.arizona.edu/~pen/ame553...son%2008-A.pdf

[Amanuensis]

La matrice R1 est celle qui permet de passer de à

R2 permet de passer de à

Il me semble, mais je peux me tromper, qu'il y a confusion entre matrice et rotation. R1 est la rotation qui permet de... (Et non la matrice.)

Ensuite, pour exprimer ces rotations sous forme de matrices, faut choisir une base. La composition des rotations correspond à la multiplication des matrices uniquement si ces matrices sont toutes exprimées dans la même base.

La matrice représentant R1 et celle représentant R2xR1 étant exprimées dans la base sans prime, la matrice représentant R2 doit aussi être exprimée dans cette base, et non dans la base prime.

[invite9c7554e3]

je pense plutot que j'ai fais une erreur de raisonnement dans le calcul n°2

car je ne pense pas avoir fait d'erreur dans les matrices R2 et R1 car si tu regardes les dessins ci dessousje trouev bien ce qu'il y a noté ci dessus :

[Amanuensis]

Je n'ai pas l'impression que vous ayez compris le point que je posais.

Dans le dessin indiqué, la rotation R2 est représentée par sa matrice exprimée dans la base prime (matrice qu'on pourrait noter M2', qui n'est pas la même que M2, la matrice représentant la rotation R2 dans la base sans prime).

Autrement dit le dessin est correct, mais cela n'amène pas à la relation matricielle exprimée dans la partie "rappels" du message #1.

[Amanuensis]

PS: Si P1 est la matrice faisant passer des coordonnées sans prime aux coordonnées prime, alors on a

M2 = P1^{-1}M2'P1

Donc M3 = M2 M1 devient M3 = P1^{-1}M2'P1 M1

A partir de ça on devrait trouver la bonne relation matricielle...

[invite9c7554e3]

Je n'ai pas l'impression que vous ayez compris le point que je posais.

effectivement, je me rend compte à lisant ton nouveau message que j'ai loupé une info

Dans le dessin indiqué, la rotation R2 est représentée par sa matrice exprimée dans la base prime (matrice qu'on pourrait noter M2', qui n'est pas la même que M2, la matrice représentant la rotation R2 dans la base sans prime).

ah OK, je vois ce que tu veux dire.

Dans le dessin indiqué, la rotation R2 est représentée par sa matrice exprimée dans la base prime (matrice qu'on pourrait noter M2', qui n'est pas la même que M2, la matrice représentant la rotation R2 dans la base sans prime). Autrement dit le dessin est correct, mais cela n'amène pas à la relation matricielle exprimée dans la partie "rappels" du message #1.

d'accord je vois ce que tu veux dire mais j'ai l'impression que lorsque je regarde des cours sur les angles d'Euler on doit bien trouver cette expression.
Je me trompe ?

PS: Si P1 est la matrice faisant passer des coordonnées sans prime aux coordonnées prime, alors on a
M2 = P1^{-1}M2'P1
Donc M3 = M2 M1 devient M3 = P1^{-1}M2'P1 M1
A partir de ça on devrait trouver la bonne relation matricielle...

Je vais regarder mais dans la première partie de la "démonstration" on ne transporte pas des coordonnées mais juste des vecteurs de base... je ne sais pas si on peut faire ceci ?

[Amanuensis]

Si P1 est la matrice faisant passer des coordonnées sans prime aux coordonnées prime, alors on a

M2 = P1^{-1}M2'P1

Donc M3 = M2 M1 devient M3 = P1^{-1}M2'P1 M1

A partir de ça on devrait trouver la bonne relation matricielle...

Je continue alors... Comme on a P1M1 = I, on obtient comme relation M3 = M1 M2', et non pas M3 = M2' M1...

[invite9c7554e3]

Tu as raison ! mais je bloque encore


Je recommence donc en essayant d'écrire la 1ere partie proprement (avec cette fois 3 rotations) :

Rotation autour de (et exprimé dans e)

Rotation autour de (et exprimé dans e')

Rotation autour de (et exprimé dans e'')

Si on veut passer de la base e''' à la base de départ e il faut utiliser cette relation :

où R3, R2, et R1 sont exprimés dans la base de départ "e".

Or il n'y a que les matrices R1,R2' et R3'' que l'on connait facilement, on va donc exprimer R2 et R3 en fonction de ces dernières par changement de base
On a, comme tu l'as dit :

or on a , et on trouve ce que tu as dis :


Maintenant on va s'intéresser à la matrice R3 en l'exprimant en fonction de R3'' que l'on connait :


Et donc :


et là je n'arrive pas à simplifier pour trouver un truc cohérent... encore moins ce qu'il y a sur ce document (p47-48): http://eavr.u-strasbg.fr/~bernard/ed...master_gsb.pdf

[invite9c7554e3]

je suis en train de me rendre compte d'un truc :

\left[P_1\right]^T\left[P_2\right]^T\left[R_3''\right]\left[P_2\right]\left[R_2'\right][/TEX]

ici les termes s'annulent puisque j'ai définit mes matrice de passage de façon relative : B vers B' et B' vers B''

Soit au final la relation qui me parait bien fausse puisqu'on a montré que et pas (chose qui m'aurait bien arrangé pour retrouver un resultat coherent)

[Amanuensis]

Tentative: on passe d'abord tout en prime:

M3M2M1 = M1 (M3M2)'

Puis on a (M3M2)' = M2' M3"

D'où M3M2M1 = M1 M2' M3"

[invite9c7554e3]

super! merci beaucoup

On trouve donc bien :


Maintenant, gros problème :

je viens de vérifier sur le net et je suis tombé sur ce cours (page 2)
http://www.u.arizona.edu/~pen/ame553...son%2008-A.pdf
et celui-ci (page 48) :
http://eavr.u-strasbg.fr/~bernard/ed...master_gsb.pdf

et la relation qu'ils trouvent est (équivalente à la notre si on choisi des angles negatifs):


as tu une idée d'où peut venir cette différence ?

[invite9c7554e3]

par contre je suis sûr que ce que l'on a fait est correct car si je refais ce que j'ai appelé "calcul 2" dans mon premier message alors je trouve le même résultat que le calcul 1 !

Du coup je ne comprends pas d'où sort la formule proposée par les autres auteurs...

[invite9c7554e3]

M2 = P1^{-1}M2'P1

Puisque P1 est définit comme la matrice permettant de passer de la base B à B' ne faudrait il pas appliquer la relation inverse :


en accord avec ce cours:
http://uel.unisciel.fr/physique/outi...e_ch11_19.html

[Amanuensis]

Puisque P1 est définit comme la matrice permettant de passer de la base B à B' ne faudrait il pas appliquer la relation inverse :

Pour moi, non, mais je peux me tromper. Le raisonnement que je fais est le suivant : si j'applique à un triplet V, M2'V = P1^{-1}M2P1V ne marche pas parce qu'à droite on a P1V ce qui demande V dans la base sans prime et à gauche on a M2'V ce qui demande V dans la base avec prime, ce qui est contradictoire. Par contre, M2'V = P1M2P1^{-1}V est correct selon ce critère, V est dans la base prime des deux côtés.

Le point d'achoppement est peut-être simplement la définition de P1. Je prends comme définition la matrice qui appliquée par sa droite aux coordonnées dans B (soit V) donne les coordonnées dans B' (soit V'), donc V'=P1V.

[invite9c7554e3]

tout d'abord merci beaucoup de prendre le temps de m'aider à comprendre ces mystères

​​​​​je crois que la différence vient de la définition de P1 car dans des cours comme celui ci :
https://tice.agroparistech.fr/course...cidReq=RAPMATH

La matrice de passage est classiquement définit comme ceci :


Donc la formule de passage devrait être:


Avec ceci penses tu que l'on puisse retrouver la relation inverse de la notre ? j'ai essayé et je n'y arrive pas... ce qui me perturbe encore plus c'est que les matrices de rotation définies dans ce cours :
http://www.u.arizona.edu/~pen/ame553...son%2008-A.pdf

Moi avec leur shéma je ne trouve pas les mêmes matrices de rotation : j'ai les matrices inverses et la meme formule :


comprends tu pourquoi nous n'avons pas les mêmes choses que dans ce document ?

[Amanuensis]

Dans le cas présent, changement de signe de l'angle = inversion de la rotation = transposition de la matrice

Et en plus le signe de l'angle dépend d'une convention.

Beaucoup de sources possibles pour cette différence, donc.

(Et je n'ai pas trop envie de regarder les docs en détail... )

[invite9c7554e3]

Oui je comprends, merci beaucoup Amanuensis pour ton aide

pour le moment je suis perdu car nous n'avons pas la même relation convention pour un changement de base ou

J'ai ouvert une discussion là dessus : http://forums.futura-sciences.com/ma...le-de-2-a.html

Dès que j'aurais compris ceci je reviendrais sur ce sujet pour essayer de conclure. Pourras tu à ce moment là jeter un coup d'oeil avec ma conclusion et me dire si tu es d'accord ?

merci pour toute ton aide et bonne année