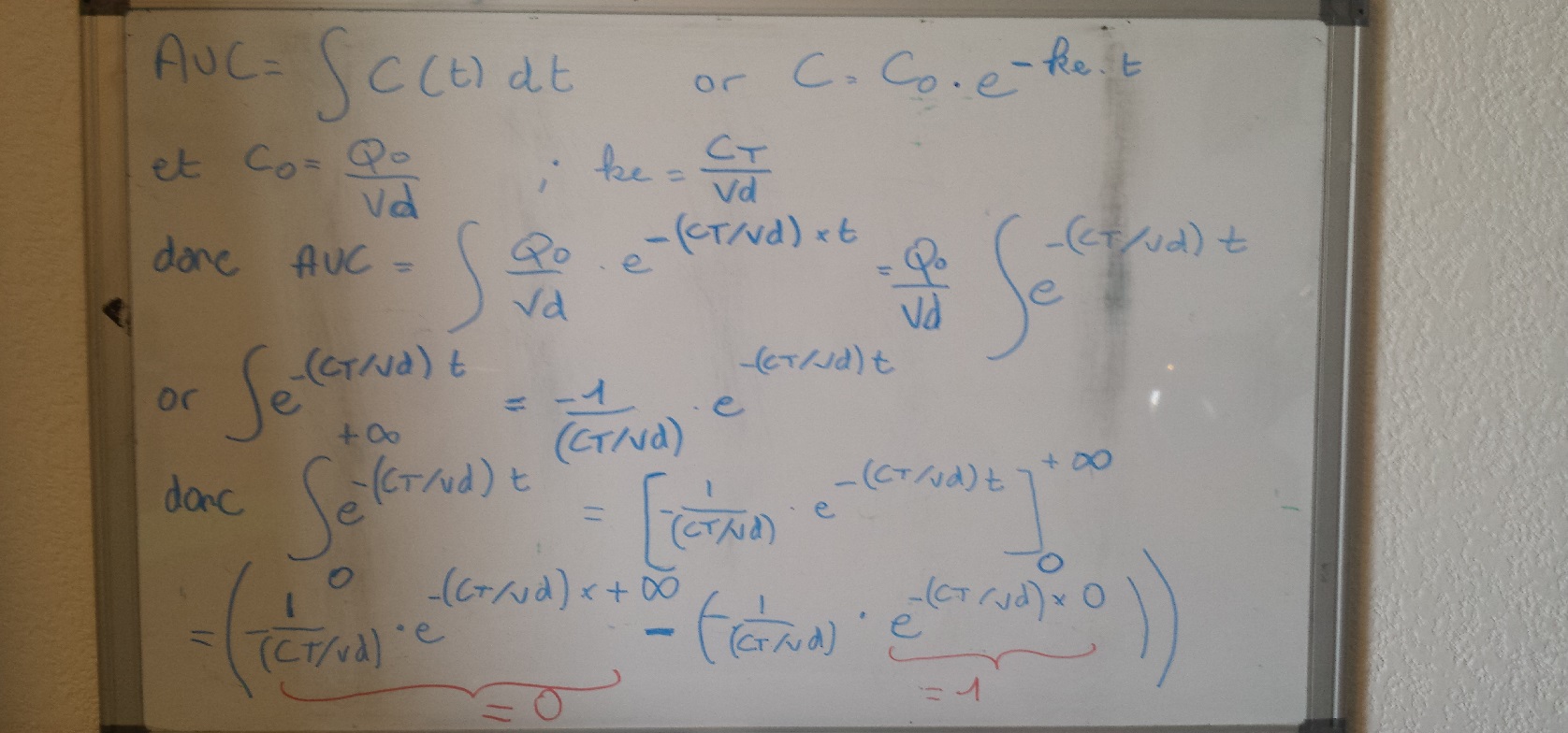Intégrale : aire sous courbe

[Quentin.B]

Bonjour,
Étudiant en Biologie, je travaille actuellement un cours de Pharmacocinétique. Dans celui-ci, une formule nous est démontrée mais je bloque à une étape.
En effet, je comprends l'ensemble des formules à l’exception de l’intégration. Je ne sais pas comment retrouver AUC=Q0/Ct en intégrant -dQ/dt.
À noter, que pour l'étape précédente, on sait que Vd=Q/C donc Ke x Q = Ke x Vd x C or Ke x Q = Ct x C donc Ct = Ke x Vd.
De plus, à t=0 on a Q=Q0 et C=C0 donc Vd=Q0/C0.
Sincèrement,
Quentin
PS : AUC = aire sous courbe (Area Under Curve)

-----

[Tryss2]

Si f est une fonction positive, l'aire entre la courbe de la fonction f (entre a et b) et l'axe des abscisses est donnée par



Après, comme n'est pas précisé quelle est la courbe dont l'aire sous la courbe nous intéresse (de Q? de C? entre quels points?), il est difficile de vraiment t'aider (sauf à jouer aux devinettes)

[Resartus]

C'est en effet très laconique, à moins que vous ne l'ayez déjà étudié avant...

La courbe de décroissance de C est exponentielle, ce qu'on peut retrouver en voyant que dC=-dQ/Vd=-C.Ct.Vd.dt soit dC/C=-Ct/Vd.dt=-ke.dt
soit d(logC)=-ke.dt, qu'on intègre log(C)= -ke.t+cste d'où la solution C=C0exp(-ke.t).
Ensuite, quand on prend encore l'intégrale de cela, on obtient [-C0exp(Ke.t)/ke] entre 0 et l'infini, ce qui fait donc une AUC égale à C0/ke

[Quentin.B]

À force de chercher on finit par trouver ! J'avais effectivement omis de vous transmettre la fonction C(t) et son équation.
Mon problème est donc résolu, merci pour votre aide et voici la solution.

De l'intégrale on a alors 1/(Ct/Vd).
On obtient alors AUC = Q0/Vd * 1/(Ct/Vd) donc AUC = Q0/Ct (cqfd).
Sincèrement,
Quentin

[A voir en vidéo sur Futura]