point d'attraction : dépendance angulaire?

[geometrodynamics_of_QFT]

Bonjour,

Je suis arrivé à la conclusion qu'en itérant une certaine opération géométrique (dans ce cas-ci, une projection stéréographique en 2D) pour un certain angle donné, la succession des points projetés (C, C', etc...) convergeaient vers un point encore inconnu.
Autrement dit, la succession des points par lesquels passent les arcs de cercles en orange sur la figure (F' --> F --> P'' -->N' --> ...)

L'unique paramètre du système est l'angle et il varie de à au cours de la transformation.
Dans la figure donc, les cercles noirs sont fixes et de dimension fixe, les cercles mauves sont fixes relativement au segment [FC] et de dimension fixe, et seuls les arcs de cercles en orange varient, il sont représentés ici pour une certaine valeur arbitraire de .

Donc lorsqu'on fait varier , seuls les segments bleu, rouge, et les arcs oranges varient en taille.

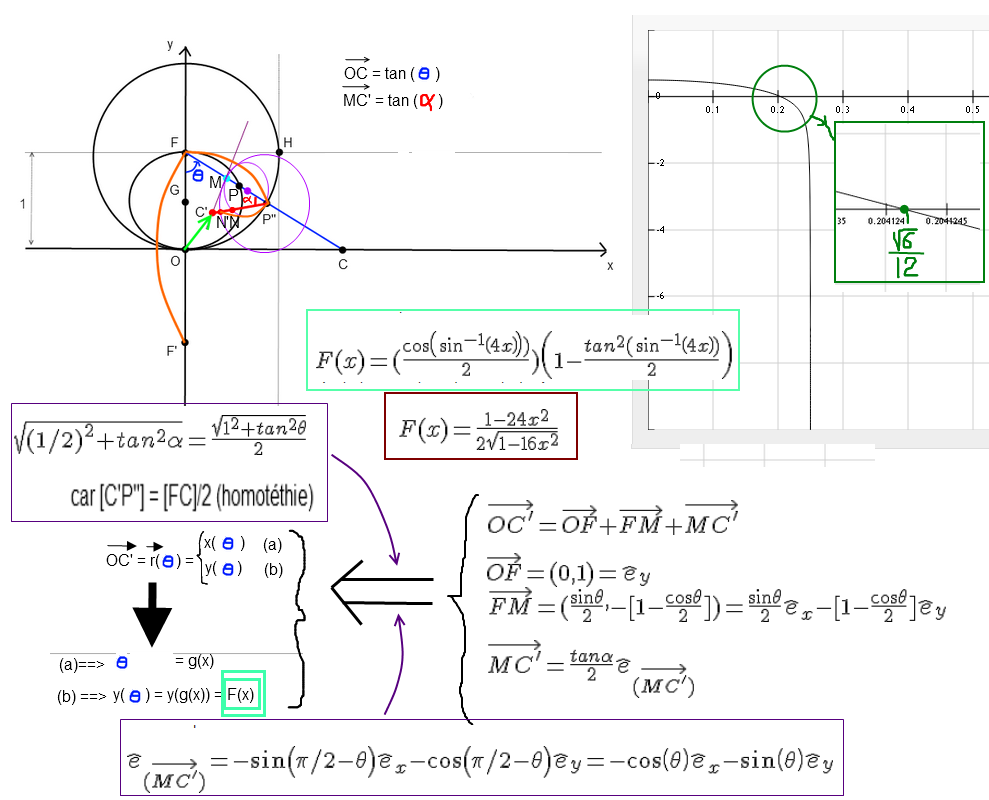
Voilà une illustration de la construction géométrique, ainsi que des arguments permettant d'obtenir l'objet d'un fil précédent, à savoir F(x) ou le lieu des points C' lorsque varie de à :


EDIT : en haut et au centre dans l'image, c'est évidemment la norme des vecteurs OC et MC' qui sont égales aux valeurs données...
Un premier point est déjà de vous demander si ces calculs sont corrects?

Ensuite, étant donné les propriétés suivantes (l'analogie des transformations dans l'itération du processus) :

• Le point C est la projection stéréographique du point P sur la médiatrice de [FF'];
• Le point C est le centre du cercle de rayon [FC] passant par F, auquel appartient l'arc orange F'F;
• Le lieu des points C est le segment de droite , car leur abscisse est donné par

_________________________

• Le point C' est la projection stéréographique du point N sur la médiatrice de [FP'']
• Le point C' est le centre du cercle de rayon [C'P''] passant par P'', auquel appartient l'arc orange FP''.
• Le lieu des points C' est le la fonction , car leur abscisse est donné par .

Comme expliqué dans l'image....

J'aimerais savoir si ces informations sont déjà correctes, si oui pertinentes, et si la situation est assez "triviale" que pour se poser la question du point de convergence de l'itération de ce processus?
Et comment se déplace ce "point d'attraction" lorsque varie?
Est-ce un domaine déjà exploré en maths?

Je vous remercie beaucoup!
-----

[geometrodynamics_of_QFT]

La convergence est dûe au fait que l'angle est plus petit que l'angle , n'est-ce pas?

[geometrodynamics_of_QFT]

De plus, concernant la limite de F(x), j'ai une autre question :

Pourquoi Lim_(x-->1/4) de F(x) = -l'infini alors que

en , , et qu'en cette valeur de , le centre C' de l'arc FP'' doit être sur l'axe , mediatrice de [FP'']!?!?
(de la même manière que le centre C est sur la médiatrice du segment [FF'])

[geometrodynamics_of_QFT]

Et enfin, dernière question :

Comme exprimée plus haut non simplifiée, la relation entre l'angle et l'angle est:

.

Peut-on en déduire une relation entre les angles entre eux directement?
Par exemple quelquechose du genre ?
Car j'imagine que ce paramètre aurait un rôle crucial pour caractériser la convergence en fonction de l'angle ?

(Chaque angle donnant lieu à un point de convergence différent, puisque tout le segment bleu (et le rouge aussi, et les suivants) pivote pendant la transformation...)

Je me demande quel est le lieu des points de convergence en fonction de ...?
Ce qui est sûr, c'est que pour , ça converge vers 1-1/2+1/4-1/8+1/16-...=? car tous les demi-cercles sont centrés sur l'axe des y.

[A voir en vidéo sur Futura]

[geometrodynamics_of_QFT]

Pour la suite de cette palpitante aventure autour du cercle, je vous donne rendez-vous sur ce fil, où l'on essaie de calculer où convergent les arcs de cercles oranges dans la construction!
Le tout, en fonction de l'unique paramètre du problème!
On se rapproche, mais il y a encore du boulot!