Bonjour !
Alors voilà j'ai un soucis lors de la résolution d'une équation avec la transformé de la place. Et même de manière général je coince un peu sur la partie décomposition en élément simple qui revient quasiment à chaque fois. J'ai seulement appris en décomposant avec a/(x-x1) + b/(x-x2) +c(x-x3) sauf que par exemple dans le cas d'un exemple d'équation sur wikipedia
https://fr.wikipedia.org/wiki/Applic...3%A9rentielles
je n'arrive pas faire la décomposition, impossible de comprendre pourquoi...
Voilà ce que j'ai fais, j'ai ajouté un deuxième exemple où la aussi je bloque complètement. je trouve B=1 mais après on m'as toujours dit je remplacer p par une valeur sauf qu'il me restera les deux inconnus A et C...
Peut-on m'expliquer la méthode à utiliser ?
Merci beaucoup
-----



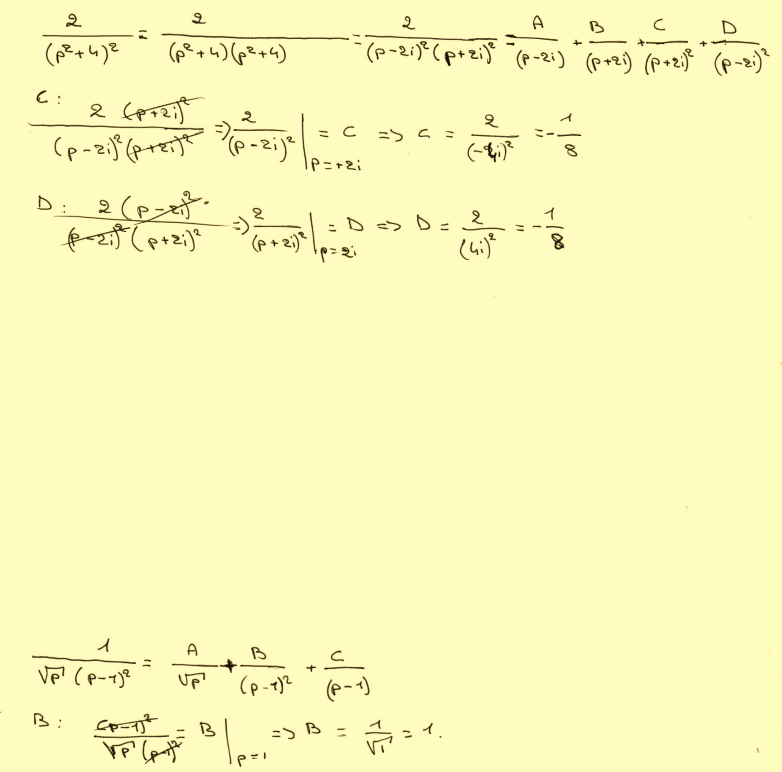
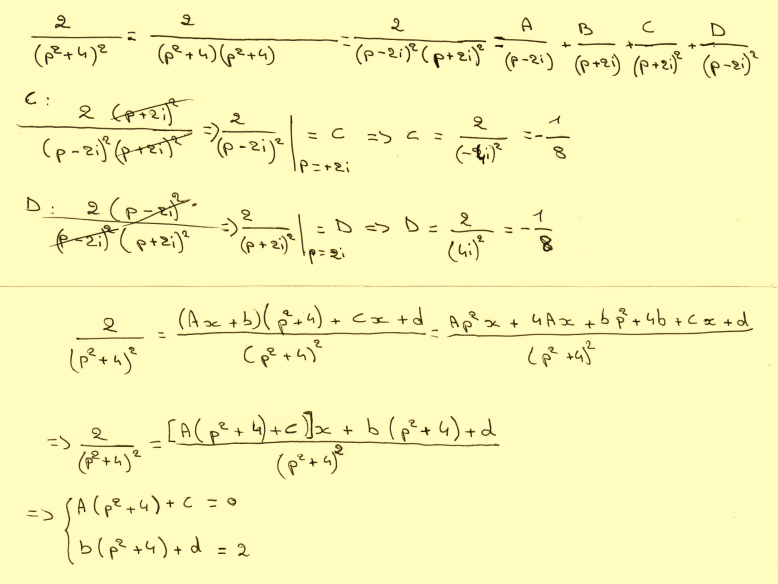


 avec une fonction de p...
avec une fonction de p...