"nombres 'englobants' ou 'ovoïdes' ; 'combinatoire et dénombrement de cercles imbriqués' "

[invite332de63a]

Je pense que la représentation en arbre enraciné proposée par Sérios simplifierait grandement la représentation... même si sur le forum elle sera difficile à écrire...
-----

[invite332de63a]

Désolé pour ce triple post...

Je pensais, pourquoi ne pas représenter ces ovoïdes par des nombres, avec les ordinaux c'est possible comme expliqué par El jj dans cette vidéo à 8 min 40 s.

Ainsi le nombre ( () ( () () ( () ) ) ) ( () () ) peut s'écrire à l'aide des ordinaux .

Je pense que pour plusieurs écritures d'un même ovoïde on obtient le même ordinal. Ce qui résout le problème des ovoïdes égaux. Peut être même que cela peut simplifier les problèmes sur la multiplication etc...

Explication en image:



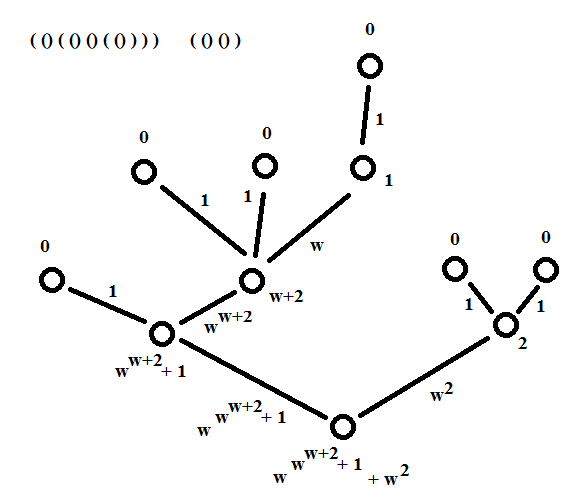
Maintenant, est-ce que tout ordinal correspond à un nombre ovoïde?? Ce qui serait dommage ...

[ulyss]

Merci Ulyss pour cet exemple de non associativité. Dommage, ça réglait le problème de 0.

D'ailleurs j'ai fait une petite erreur à un moment... je vous laisse la découvrir , mais elle ne change pas le fait que les résultats sont différents...

Concernant vos différentes écritures d'un même ovoïde, il me semble que seule l'écriture :



vérifie l'exigence de classement décroissant des sous-ovoïdes...

Après autre question que vous évoquez à mots couverts :
Pour un même "nombre" ovoïde, combien d'écritures différentes?

[ulyss]

Maintenant, est-ce que tout ordinal correspond à un nombre ovoïde?? Ce qui serait dommage ...

Oula en effet, j'ai visionné la vidéo... donc si tout ordinal correspond à un nombre ovoïde... alors toute notre petite "théorie" doit exister depuis longtemps...

[invite332de63a]

Je n'ai pas la démo claire mais je pense que ce procédé donne une bijection qui respecte l'addition mais ta multiplication est belle et bien distincte de celle usuelle sur les ordinaux. À voir si cela peut nous permettre de dénombrer tes nombres avec un nombre d'ovoïdes fixé.

[ulyss]

Si j'ai bien compris, avec la représentation sous la forme d'ordinaux transfinis et celle introduite par Mediat, voici quelques exemples :

1111 = ()() ~ 2

22 = (()) ~ .

2112 = (()()) ~ .

211211 = (()())() ~

43111112431112 = (((()))()()())(((()))()()) ~ .

Bon ensuite la relation d'ordre sur les ordinaux est a priori la même que celle que j'ai définie sur les ovoïdes (c'est sympa çà, mais à préciser pour être sûr)
ainsi comme on a ((())) > (()()) d'après la définition que j'ai donnée on a aussi :
.
en constatant que ce sont les ordinaux qui correspondent aux deux ovoïdes proposés.

Ensuite l'addition des ovoïdes correspond à l'addition des ordinaux de manière assez évidente.

Mais pour la multiplication, ce n'est pas la même chose!! (ouf)

Ainsi :

22 * 1111 = (()) * ()() = (()()) correspond à .

mais .

Donc on a un contre-exemple...

[ulyss]

43111112431112 = (((()))()()())(((()))()()) ~ .

Erreur , c'est plutôt
43111112431112 = (((()))()()())(((()))()()) ~ .

Désolé je fatigue...

[ulyss]

J'ai la bizarre impression que ma définition de la multiplication sur les nombres ovoïdes correspond en fait juste à l'élévation à la puissance sur les nombres ordinaux...

Ainsi :
((())) * (())(()) = (((())(())))~

et:
élevé à la puissance

De la même manière :

((())) * (())(())(()) = (((())(())(())))~

et
élevé à la puissance

Ainsi forcément * n'est pas commutative tout comme l'élévation à la puissance ne l'est pas...

Néanmoins l'élévation à la puissance est associative pour les ordinaux! Donc il y a une "couille" dans le potage car * n'est pas associatif sur les nombres ovoïdes...

En effet :

(()()) * (()) = ((())(()))~

et
élevé à la puissance donne

Donc dans le cas général la multiplication * des ovoïdes ne correspond pas à l'élévation à la puissance sur les ordinaux correspondants...

Bon du coup on peut quand même dire a priori que la multiplication à gauche par un ovoïde du type ii avec i entier correspond à l'élévation à la puissance de ii ~ (élevé (i-1) fois à la puissance ) par l'ovoïde de droite.
ii * Y ~ (élevé (i-1) fois à la puissance ) puissance (~Y)

avec ~Y = ordinal correspondant à Y

[ulyss]

Avec les ordinaux, tout devient plus simple en fait...

on peut écrire les résultats suivants, avec X nombre ovoïde quelconque (çà marche même si X est le vide) :

()() * X = 2X

(()) * X ~

(()()) * X = (XX) ~

((()())) * X = ((XX)) ~

((()())()) * X ~

((()()()())) * X ~

que l'on peut aussi décomposer ainsi :
((()()()())) * X = ((())) * ()()()() * X ~ * =


On a aussi comme autre exemple :
(((()()()))()()) * X = * = (((XXX)))XX) =

que l'on peut aussi décomposer ainsi :
(((()()()))()()) * X = (()) * ((()()()))()() * X
= (()) * [((()()())) + ()()] * X
= (()) * [[ ((()()())) + ()()) ]*X] car, pour tout i entier, on a [ii * X] *Y = ii * [X*Y] de manière évidente
= (()) * [ ((()()())) * X + [()() * X]] car * est distributif par rapport à + à droite : (X+Y)*Z = X*Z+ X*Z de façon aussi assez évidente
= (()) * [((XXX))XX]
= (((XXX))XX)
~

Voilà pour des exemples simplifiant le maniement de la multiplication et de l'écriture des nombres ovoïdes...

[ulyss]

C'est marrant, est a priori défini (on identifie ici X à son ordinal ~X )

Mais, a priori, ou [avec I entier=()()...() et 3 =()()() ] ne sont pas a priori définis pour tout ovoïde X !
(on n'a pas défini l'élévation à la puissance entre ovoïdes X^Y pour tout X et Y ovoïdes)

Tout cela doit probablement venir des règles d'écritures sur les nombres ordinaux transfinis...

Bon si je suis en train de réinventer le fil à couper le beurre, ou si je m'égare, prévenez-moi...

[ulyss]

Bon en fait je crois que si on considère les arbres enracinés X' et Y' associés à 2 ovoïdes X et Y,
alors le produit X * Y défini précédemment consiste uniquement à greffer l'arbre Y' sur chaque sommet (ou pointe) de l'arbre X'. (mais en "fusionnant" chaque fois la pointe et la racine)
Voilà qui simplifie tout...

[ulyss]

Tandis que l'addition X + Y consiste à greffer l'arbre Y' sur la racine de l'arbre X' en fusionnant les deux points racines...

[Médiat]

dans cette vidéo

Bonjour (et merci pour ce lien),

Presque très belle vidéo, on avait parlé du sujet là : http://forums.futura-sciences.com/de...ml#post5364812.

Mais, cette vidéo se termine par une HORREUR : il y est question de l'ensemble des "théorèmes démontrables", ce qui est un affreux pléonasme, mais surtout de l'ensemble des "théorèmes vrais de l'arithmétiques de Peano", distinct du précédent, ce qui n'a aucun sens !l

Autre erreur : le cardinal des réels n'est pas , mais ce qui n'est pareil qu'avec HC

[invite6bfdf32a]

Oui, c'est pourquoi j'ai écrit que toutes les suites n'étaient pas valides, mais l'idée n'était pas de trouver un isomorphisme entre ovoïdes et ces suites, mais une représentation permettant de faire des démonstrations

Je n'ai pas compris non plus la notation sur OEIS

Je pense que c'est la notation de Neveu.

[Médiat]

Bonjour,

Ensuite l'addition des ovoïdes correspond à l'addition des ordinaux de manière assez évidente.

Non, c'est facile à voir : l'addition des ordinaux n'est pas commutative !

[Médiat]

Je n'ai pas regardé tous les détails, mais je ne serais pas surpris que l'addition soit celle des ordinaux de Hessenberg, et bien sûr, il faudrait regarder la multiplication

Voir par exemple le chapitre VI.3 : http://forums.futura-sciences.com/ma...ml#post3958180

[ulyss]

Bonjour,

merci à tous:
- Redrum13 pour avoir parlé de la notation de Neveu
- Roberto-Bender pour avoir réintroduit la représentation en arbres enraciné et l'utilisation des ordinaux transfinis pour les représenter
- Mediat : pour tout et pour m'avoir préciser les règles de calcul des ordinaux transfinis, et pour votre dernière idée... J'avais consulté le document "Futura Science" décrivant les divers ensembles de nombres il y a quelques temps déjà... très intéressant comme document.
- et les autres...

Effectivement Médiat l'addition des ordinaux n'est pas commutative ...
Si j'ai bien compris on n'a pas :

D'ailleurs je me demande si est bien défini...

Je crois que les nombres ordinaux sont définis par des applications ou des suites sur certains ensembles... il faut que je creuse le domaine pour bien le comprendre.

Je crois que j'ai fait pas mal d'erreurs d'écriture des ordinaux dans mes posts...
Ainsi j'ai identifié à
Ce qui est faux je crois...

Tiens question basique:
Les écritures
; ;

Ont-elles un sens?

Sinon j'ai fait une erreur dans mon post qui mettait en relation la multiplication * des ovoïdes par une opération de "greffe" des arbres enracinés...
a revoir donc...
Dire que Serios avait évoquer cette représentation en arbres enracinés dès le premier post réponse... il m'aura fallu du temps pour y revenir...

Bon j'imagine que de nombreuses théories ont été développées sur la façon de combiner ou "greffer" des arbres enracinés (ou pas) les uns avec les autres...
Une de ces théories doit probablement correspondre à ces opérations sur les nombres ovoïdes... Vous avez des idées là-dessus?

J'aimerai bien comprendre la formule de récurrence que vous avez donné, Médiat, ... sa démonstration.
Car cette démonstration doit probablement donner tous les élément pour comprendre et décrire la structure des nombres "ovoïdes" et la façon dont on les génère...

Sinon j'ai une autre idée pour redéfinir ces ovoïdes d'une autre façon, et vous allez être contents : cette nouvelle façon rend le vide absorbant à droite pour la multiplication!!

[Médiat]

Bonsoir,

Exact

D'ailleurs je me demande si est bien défini...

Oui, c'est tout simplement égal à

Les écritures
; ;

Ont-elles un sens?

L'exponentiation ordinale est bien définie, mais pas la division ni la soustraction (on peut donner une définition, sans grand intérêt, dans quelques cas particuliers)

J'aimerai bien comprendre la formule de récurrence que vous avez donné, Médiat, ... sa démonstration.
Car cette démonstration doit probablement donner tous les élément pour comprendre et décrire la structure des nombres "ovoïdes" et la façon dont on les génère...

De quelle récurrence parlez-vous ?

[Médiat]

Une précision : mes réponses ci dessus (à propos de la division et de la soustraction concernent les opérations ordinales, dans certains ensembles, on peut faire des choses approchantes (les surréels, par exemple)

[ulyss]

Mediat :

Je parlais de la formule de calcul par récurrence qui permet de trouver le nombre a(n+1) de figures
de cercles imbriqués (nombre d'"ovoïdes") à (n+1) cercles en fonctions des a(i) pour i<n+1 :



signifie "d divise k"

Sinon l'écriture a un sens vous dites?

L'ordinal je comprends ce que c'est, c'est le premier ordinal supérieur à tous les ordinaux entiers naturel.
L'ordinal aussi, c'est le premier ordinal supérieur à tous les avec i entier
L'ordinal est le premier ordinal supérieur à tous les ordinaux de la forme avec i, j entiers (tous ces ordinaux sont bien totalement ordonnés.)

Mais , qu'est-ce que c'est?
En toute logique ce devrait être le premier ordinal supérieur aux avec i entier(qui sont totalement ordonnés)...
Or ces sont tous des ordinaux entiers...
Donc en toute logique on devrait avoir:

Non?

Mais n'est pas divisible par trois car la division des ordinaux n'est pas définie...

or tous les éléments sont divisibles par trois... donc on aurait une suite de nombres tous divisibles par trois qui se terminerait par un nombre non divisible par trois, bizarre...

Je pense que la réponse est peut-être qu'en fait, même sur les ordinaux entiers normaux : 3 ; 9 ; 27 ; 81 ; etc... la division n'est pas définie... Ce doit être cela la bonne réponse... la division n'est sûrement définie que pour les cardinaux, qu'ils soient finis ou infinis...

[Médiat]

Attention, l'exponentiation ordinale n'a rien à voir avec l'exponentiation cardinale : chapitre VI.1 du même document ...


Pour la formule, je n'ai pas la moindre idée de sa démonstration, malheureusement

[ulyss]

Merci
J'ai regardé rapidement, en particulier on a :


donc :


comme je l'avais écrit.

[ulyss]

Bon je compte ici vous présenter ma nouvelle définition des nombres ovoïdes...

A la base la première définition vient du fait que l'on combine deux "opérations" primordiales de bases que sont la juxtaposition
et l'englobement ou entourage ou inclusion.

Les nombres entiers usuels ne sont définis qu'en utilisant la "juxtaposition"
Les ovoïdes initiaux sont obtenus en combinant juxtaposition et inclusion.

L'ensemble vide est associé au zéro.

Seulement voilà... englober un ensemble vide cela n'a pas beaucoup de sens..
Autrement dit l'ensemble qui contient uniquement l'ensemble vide n'a pas grande signification, ... c'est aussi lui-même l'ensemble vide
me semble-t-il
Une "bulle" qui ne contient rien "éclate" et se résoud en du vide.

Ainsi, avec cette nouvelle approche, l'ovoïde () est le même ovoïde que le vide.
De même ()() (()) (())() ou autres ne sont que des "bulles" qui ne contiennent rien au final et "éclatent" naturellement
pour donner du vide... tous ces nombres "ovoïdes" ou "englobants" sont égaux au vide...

Pour pallier tout cela on définira un nouvel élément primordial : la graine, ou le point .

Cette graine symbolise l' "existence" même, le fait que quelque chose existe plutôt que du néant. (désolé pour l'image "philosophique")

Par contre on pourra englober une graine... cela a du sens.
ainsi (.) existe.
de même ces nouveaux ovoïdes engrainés existent :
((.))
(.)(((.)))
(.(.))
((.)(.))
etc..

On a aussi les séries de "graines" :
.
..
...
etc.

Ces graines juxtaposées seront associées aux nombres entiers usuels.
1 = . 2 = .. 3 = ... etc.

On redéfinit l'addition par la juxtaposition (ou concaténation) d'ovoïdes...
((.)) + (...) = ((.))(...)

On redéfinit la multiplication par le remplacement de toute graine de l'ovoïde de gauche par l'intégralité de l'ovoïde de droite:
. * (.) = (.)
((.)) * (.)(.) = (((.)(.)))
(.)(.) * (((.).)) = ( (((.).)) ) ( (((.).)) )

Avec de telles définitions, 1 = . est neutre à gauche et à droite

Le vide 0 est absorbant à gauche (X est un ovoïde quelconque):
0 * X = 0

Et, suprême délice (rires), le vide est absorbant à droite :
En effet, par définition :
((.))(.) * 0 = ((0))(0)

Or on a là des "ovoïdes" n'englobant que du vide, et donc, par définition, ils "éclatent" et donnent du vide :
((.))(.) * 0 = (())() = 0

Sympathique, non?

On a la commutativité de l'addition de manière assez simple.

La multiplication n'est toujours pas commutative :
((.)) (.) * (.)(.) = (((.)(.))) ((.)(.))
(.)(.) * ((.)) (.) = (((.))(.)) (((.))(.))
qui sont différents l'un de l'autre...

Pas d'associativité non plus pour la multiplication:
[ (.) * (..) ] * (.) = ((..)(..)) * (.) = (((.)(.))((.)(.)))
(.) * [ (..) * (.) ] = (.) * ((.)(.)) = (((.)(.)))

La multiplication est a priori distributive à droite sur l'addition, mais pas à gauche.

Avec des représentations en arbres, on représente tout çà par des arbres non forcément enracinés...
Chaque arête de l'arbre représente une inclusion ou un englobement.
Les feuilles de l'arbre desquelles ne partent aucune arête sont les graines (ou on dira fruit pour ces sommets qui sont tenus par une branche et d'où ne
partent aucune branche)
L'appellation fruit est sympa (meilleure que feuille) car un fruit, botaniquement parlant, c'est une graine en développement.

L'addition des ovoïdes à graines correspond juste à la juxtaposition des arbres (non forcément enracinés) correspondants.

La multiplication de deux ovoïdes engrainés X et Y : X * Y
soit n le nombre de feuilles ou de fruits de X (en comptant les graines isolées qui sont des racines toutes seules, c'est le nombre total de graines de l'ovoïde X)
- Si l'arbre de gauche Y' est enraciné (il a un tronc unique) on le greffe n fois directement sur chaque feuille de X' (sa racine fusionne avec chaque feuille ou graine isolée)
- Si l'arbre de gauche Y' est mutilple à m troncs Yi ( non connexe, plusieurs racines), alors on prend chaque fruit f de X'(même les fruits-racines),
on le "supprime" et on relie directement les Yi au noeud inférieur auquel était relié le fruit f, et si f est un fruit racine isolé de X', on le remplace par une copie de Y'.

Bon bref.

Cette définition est-elle plus intéressante que l'autre?
L'embêtant c'est qu'on introduit un nouvel élément, la graine.
L'amusant c'est que cela rend le vide absorbant à droite.

Maintenant, question:
Pour un nombre n de graines et m d'ovoïdes englobants, combien d'ovoïdes à graine possibles?
Ou pour un nombre n de fruits (y compris les fruits isolés) et m branches, combien d'arbres possibles?
Du coup cette fois on va peut-être bien retomber sur le nombre de catalan ou une de ses variantes...

merci pour vos réponses et éventuelles remarques

Yann

[Médiat]

Bonjour,

Autrement dit l'ensemble qui contient uniquement l'ensemble vide n'a pas grande signification, ... c'est aussi lui-même l'ensemble vide
me semble-t-il

Ah non, c'est complètement faux, l'ensemble qui contient l(ensemble vide contient un élément (d'ailleurs il correspond à l'ordinal 1)

[invite6bfdf32a]

Je suis ce post avec attention, j'ai qques idées, quand j'aurai le temps (je suis en plain déménagement lol), je creuserai une intuition que j'ai en tête.

Cordialement.

[ulyss]

Bonjour,
Ah non, c'est complètement faux, l'ensemble qui contient l(ensemble vide contient un élément (d'ailleurs il correspond à l'ordinal 1)

Effectivement j'ai fait une erreur... J'ai identifié l'ensemble vide au rien, au néant, ce qui est conceptuellement faux.
L'ensemble vide est l'ensemble qui ne contient rien, mais ce n'est pas le néant lui-même.
J'ai considéré que = {} = Rien

et avec çà {} = {Rien} = {} =
Ecritures et égalités qui sont toutes fausses.

Mais cela n'était énoncé dans mon post que de manière anecdotique dans la définition des ovoïdes avec graine, où la notion principale est que l'on introduit l'élément graine et que l'identifie les ovoïdes sans graine () ; ((())); ()() ; etc.. à , le tout uniquement afin de rendre absorbant à droite pour la multiplication.
D'ailleurs, après réflexion, cette dernière définition des ovoïdes avec graine n'apporte rien.
Elle consiste juste à remplacer les "petits cercles ne contenant rien" de la première définition par des graines .
En fait on peut juste garder la première définition et poser que est absorbant à droite pour la loi *, et alors on obtient l'équivalent des ovoïdes engrainés.

[invite9dc7b526]

J'ai considéré que = {}

ça c'est correct.

= Rien

Rien n'est pas un concept mathématique donc cette partie n'a pas de sens en maths.

[invitecb7c417d]

Bonsoir,

Bonsoir,

L'exponentiation ordinale est bien définie, mais pas la division ni la soustraction (on peut donner une définition, sans grand intérêt, dans quelques cas particuliers)

Sans grand intérêt (dites-vous ?), j'aimerai bien savoir pourquoi ?
Si je reprends l'expression de l'addition non commutative , alors la "soustraction" doit avoir un sens ? Non ?

càd puisque c'est non commutatif ? Et que ça doit être équivalent ?

J'ai suivi (vite fait, d'où l'emploi du présent de l'indicatif ), de loin, désolé !

Si l'ordinal d'un ensemble infini (cardinalité infini donc) est infiniment défini (ordinaux d'équivalence ?), il en va de même pour les topologies** (ici les ellipsoïdes me font penser aux orbites de tout les astres, qui sont des coniques, dans l'univers observable (au moins*), cependant sa "platitude" défini par "défaut" pourrait n'être "possible" (je dirai bien réel, mais dieu m'en empêche ) que par principe d'identité, une courbure ne pouvant s'extraire que par définition d'une identité = (proche) de la courbure actuelle, avec variations autour ... ) ; donc, la courbure doit pouvoir osciller entre la concavité & la convexité ... sans jamais atteindre "l'exactitude de la planification plate"*** (Euclide est dépassé depuis longtemps )

* : principe de Mach
** : l'ensemble univers (si on le considère fini, en nous y incluant, donc fermé !), se contient lui même, obligatoirement donc ! Ce qui signifie qu'il n'a pas à proprement parlé, un choix infini de topologies (puisqu'elles sont sécantes/connexes), non ?
*** : sans exclure de solutions arbitrairement (dixit infini vs fini).

PS : D'ailleurs la courbure de l'univers est notée

PS2 : hum, je dois être ailleurs ... j'ose à peine poser la question (mais bon, ça n'ajoutera jamais qu'à mon pédigrée, pâle , une connerie de +, puisqu'il parait que le symétrique de l'addition pour les entiers relatifs, ne peut être défini pour les ordinaux )

PS3 : Désolé, j'utilise volontiers, des termes Physiques, c'est sans aucun doute ? Pas bien défini "ici" !

[Médiat]

Bonjour

Déjà, ça, c'est faux, est égal à ...

[invitecb7c417d]

Bonsoir Médiat, déjà méaculpa pour cette GROSSIÈRE erreur, j'étais parti de :

Oui, c'est tout simplement égal à

Pour

Et donc (erreur de retranscription surtout que j'avais bien en tête "l'ordre" d'écriture puisque ce sont des ordinaux, et donc faire gaffe à la non commutativité ) ; je voulais marquer

Déjà, ça, c'est faux, est égal à ...

Donc alors oui, si l'affirmation de ma négation reste exact (Je m'attaque à ça ... car je suis une bille en maths, remarque que jouer aux billes en maths, ça serait + simple non ? Quoique ? ), j'irai jusqu'à écrire que , mais je n'en suis pas sûr du tout (pour le coup ?) ?

Et donc, je conclus sur ça : si ce que je tente vainement de rectifier s'avère totalement faux, mais je veux dire que j'accepte la correction, ce n'est pas la peine d'aller + loin ! Car je suppose que le reste est du même tonneau pour vous ?

Mais au moins, j'aurai appris quelque chose & en cela je vous remercie de m'avoir laissé une chance !

Bon, bah à dans 50 ans quand je commencerai l'arithmétique rythmique sur des support algorithmique sur des machines de Turing quantique

PS : Le fond de mon questionnement est de savoir "pourquoi" l'addition ne serait pas la même opération qu'il s'agisse d'entier relatif, donc avec un signe - attaché comme identité, qu'avec une véritable "soustraction" et un signe - qui ne soit <=> à l'addition + ; dans le cas des ordinaux ?

PS2 : Désolé si je m'exprime comme un pied je devrais peut être entamer une carrière de footballeur