Bonjour, j'ai ici deux exercices pour lesquels je suis bloqué:
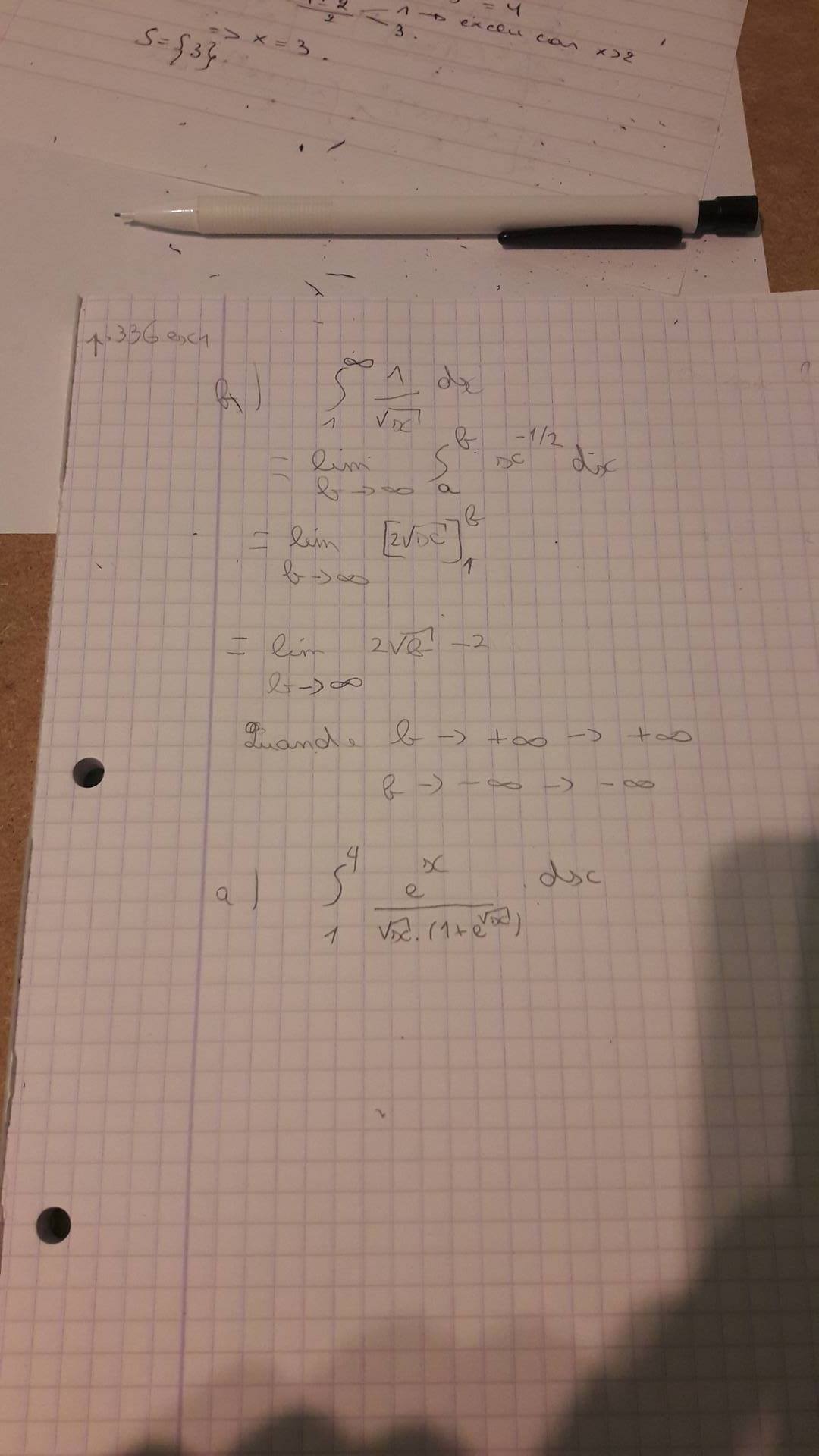
le premier, j'ai trouvé une réponse mais je ne suis pas certain qu'elle est correcte car je ne comprends pas l'intérêt de poser b si c'est pour trouver ce genre de réponse au final. (Quand je mets " Quand b - > + l'infini - > l'infini, la deuxième flèche signifie la réponse en fait)
Le deuxième, je ne sais absolument pas quoi faire... J'ai vu que certains de mes camarades ont posé u = 1 + eracine x , sauf que même en faisant cela, je suis bloqué puisque je ne sais pas comment réécrire le numérateur ensuite (sans parler de trouver la valeur de du ..). Sauriez-vous m'aider?
-----



