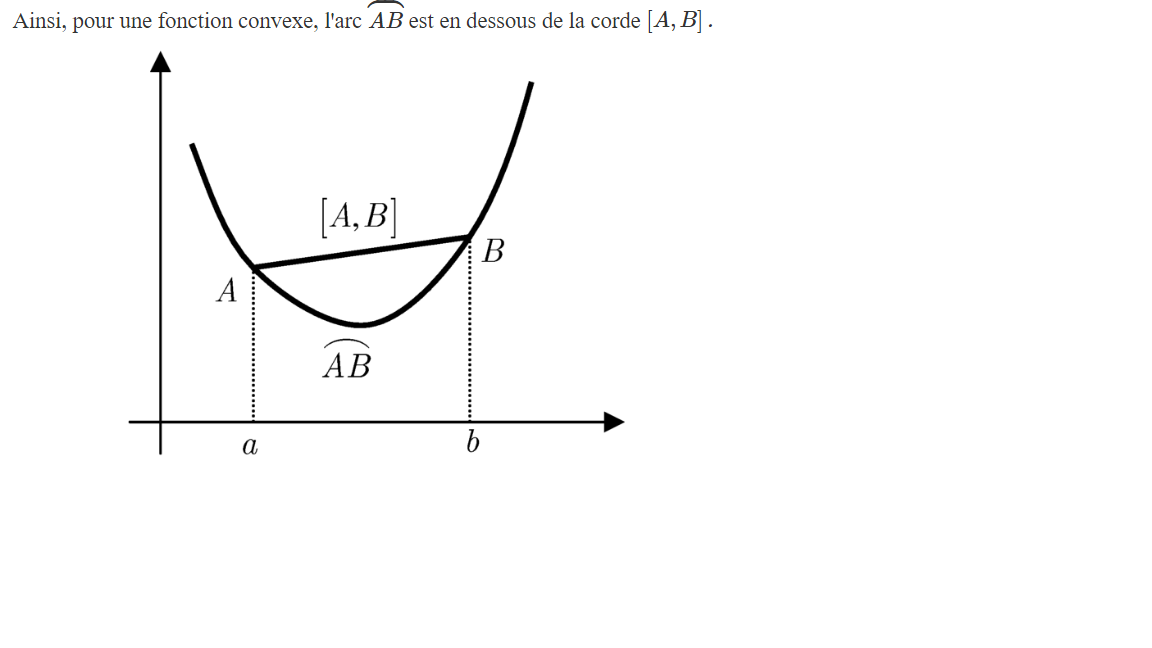
Bonsoir,
J'ai du mal à comprendre la notion de convexité à partir de cette formule :
Une fonction f : I-> R est convexe si elle vérifie pour tout a,b appartenant à I, pour tout lambda compris entre 0 et 1 :
Ce graphe permet de mieux comprendre mais je comprends pas pourquoi comment on obtient :
Merci
Bonjour.
Soient a et b deux nombres, avec par exemple a<b. Représente l'ensemble des nombres (1-k)a+kb pour k variant de 0 à 1 (tu peux commencer par des valeurs particulières de k, puis trouver ce qu'il est, puis prouver ce que tu as vu.
Ensuite, tu pourras comprendre comment est obtenu l'arc AB, en rectifiant ce que tu as écrit (c'est xA et xB à la place de A et B), puis t'attaquer aux points du segment AB.
Bonne réflexion personnelle !
En prenant des exemples, j'ai remarqué que pour a<b avec k compris entre 0 et 1 :Envoyé par gg0
ka+(1-k)b est toujours compris dans l'intervalle [a;b]
Après je pense que si on prend un x=ka+(1-k)b alors l'arc AB a pour image f(x)=f(ka+(1-k)b) c'est correct ?
Ensuite pour le segment AB je bloque ....
Je comprends pas pourquoi le segment AB a pour image : g(x)=kf(a)+(1-k)f(b) ???
Bonjour.
" j'ai remarqué que pour a<b avec k compris entre 0 et 1 : ka+(1-k)b est toujours compris dans l'intervalle [a;b] "
En fait, c'est plus général. Pour tout k entre 0 et 1, a<= ka+(1-k)b est t<=b (preuve assez simple en remplaçant b par a pour la première inégalité, et a par b pour la deuxième).
Réciproquement, si, alors
En posant
Bilan : Pour a<b, l'ensemble
Pour le segment [AB], c'est la même idée que celle que tu as utilisée, avec la fonction affine convenable, ou bien une application simple du théorème de Thalès pour trouver l'ordonnée du point d'abscisse ka+(1-k)b.
Dans les deux cas, un très bon niveau de seconde suffit.
Cordialement.
Merci.Bonjour.
" j'ai remarqué que pour a<b avec k compris entre 0 et 1 : ka+(1-k)b est toujours compris dans l'intervalle [a;b] "
En fait, c'est plus général. Pour tout k entre 0 et 1, a<= ka+(1-k)b est t<=b (preuve assez simple en remplaçant b par a pour la première inégalité, et a par b pour la deuxième).
Réciproquement, si
En posant
Bilan : Pour a<b, l'ensemble
Pour le segment [AB], c'est la même idée que celle que tu as utilisée, avec la fonction affine convenable, ou bien une application simple du théorème de Thalès pour trouver l'ordonnée du point d'abscisse ka+(1-k)b.
Dans les deux cas, un très bon niveau de seconde suffit.
Cordialement.
Je vois pas du tout où utiliser le théorème de Thalès dans ma figure.
Je vois pas comment calculer l'image de ka+(1-k)b pour le segment [AB]....
Essaie encore ...
Quand on est dans le supérieur, utiliser des notions de fin de collège ou début de lycée ne devrait pas poser de problème. Encore faut-il vouloir chercher.
Bah le segment [AB] a pour coordonnées : (b-a) et (f(b)-f(a)) je vois pas comment relier ça au : x= ka +(1-k)b
En général, dès le début du lycée, on sait que les mots coordonnées concernent les points et les vecteurs, pas les ensembles de points(droite, cercle, segment, disque, ...).
Si tu te contentes de mettre n'importe quel mot sur n'importe quelle notion, tu n'es pas près de faire des maths correctement.
Donc soit tu fais un dessin du segment, tu vois ce qui se passe, et tu appliques le théorème de Thalès, soit tu utilises l'équation de la droite (AB) pour trouver l'ordonnée en fonction de l'abscisse, mais en tout cas, tu fais des maths (application des règles que tu as eues à apprendre en troisième et seconde). Si tu ne connais pas les notions de début de lycée, apprends-les enfin, tu en as besoin.
Vu que j'ai pas capté où utiliser Thalès ici je vois qu'un segment [AB] et une courbe je vois pas le rapport avec Thalès.
Je fais avec l'équation de la droite (AB) :
Après je suis bloqué pour trouver l'ordonnée à l'origine.
Tu connais deux points de ta droite, un seul suffit. Et il vaut mieux éviter de multiplier les noms xA, c'est a, xB, c'est B.
Pour Thalès, une parallèle à l'axe des x en A te donne une configuration de troisième.
