Bonjour
Il faut résoudre cette équation-ci :
Il s'agit de la dérivation par rapport à X de l'entropie de Boltzmann-Shannon (linéairement, celle-ci s'écrit Kb*P*In (1/P)), avec Kb la constante de Boltzmann, P une probabilité, N le nombre de particule, X une longueur, T la température.
Le but est d'insérer la variable X dans P (donc trouver une valeur de P en fonction de X), afin que par dérivée, on obtienne la valeur N*Kb*T/X, comme vous le voyez sur l'image si-dessus.
C'est urgent. Merci d'avance.
-----




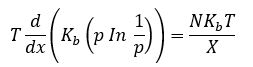
 qui est une constante, non ?
qui est une constante, non ? ) mais cela ne me permettait pas de trouver p. Appliquons toutefois ce que vous dites :
) mais cela ne me permettait pas de trouver p. Appliquons toutefois ce que vous dites :