différentielle et intégration

[fabio123]

Bonjour,

je m'intéresse, a travers une simulation que j'ai développé, au transport d'un vecteur sur une surface sphérique. En tenant compte de l'équation des géodésiques, j'arrive à exprimer les variations des composantes du vecteur dans la base locale tangente :

Expression générale :




d'où les 2 équations :



avec les composantes qui sont les composantes contravariantes du vecteur transporté.

Dans mon programme, je calcule de manière géométrique les composantes de ce vecteur, j'ai donc un tableau de coordonnées qui contient ces 2 composantes v^{\theta} et v^{\varphi} le long du transport selon la géodésique.

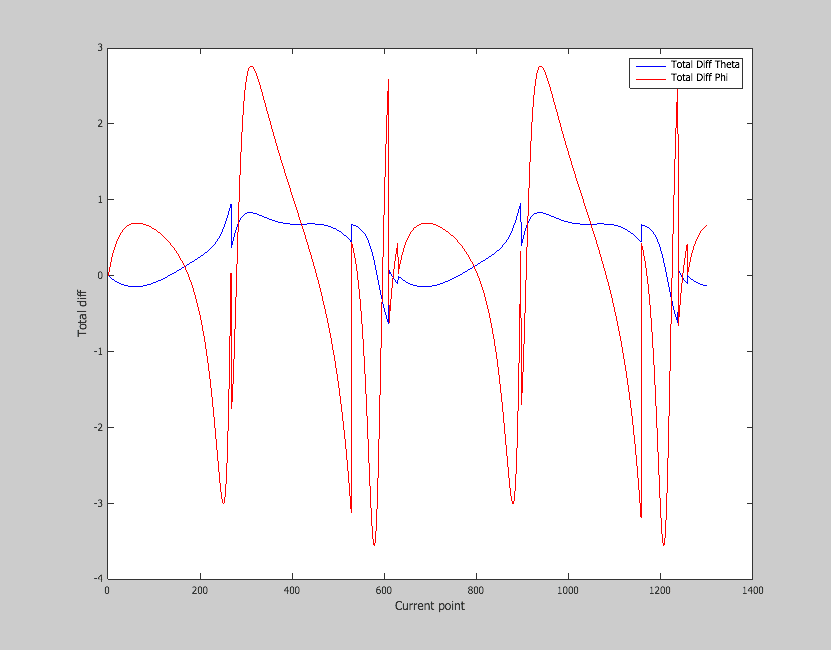
Mon problème est que je n'arrive pas à vérifier les 2 équations ci-dessus (1) et (2) : je pars d'une valeur initiale des composantes du vecteur transporté (v^{\theta}_{0}, v^{\varphi}_{0}) et en fonction des angles \theta et \varphi courants, je calcule les termes de ces 2 équations (qui doivent être égales à 0) : comme résultat, j'obtiens des valeurs numériques entre -0.4 et + 0.4 pour l'équation (1) mais par contre j'ai un intervalle de valeurs beaucoup plus grand pour (2).

Concrètement, pour obtenir ces valeurs numériques, je fais dans mon programme pour l'équation (2) :



Est-ce la bonne méthode pour calculer la valeur numériques de ces 2 équations. Je dois préciser que les 2 équations (1) et (2) sont l'expression de la dérivée covariante du vecteur transporté qui est précisée au début du post :



J'essaie de faire le lien entre les équations (1) et (2) et les formes différentielles exactes que l'on rencontre en Physique car si c'est une différentielle totale exacte, je pourrais ne m'occuper que des états initiaux et finaux quand j'intègre. Cependant, l'équation (2) ne s'apparente pas à une différentielle totale exacte car il y a la présence simultanée des termes et .

De plus, je dois aussi préciser que je travaille avec des composantes contravariantes et des problèmes de normalisation pour le vecteur e_{\varphi} peuvent peut être fausser les résultats (avec un facteur 1/R pour e_{\theta} et 1/(R sin(\theta) pour e_{\varphi}).

Toute aide est la bienvenue

ps: les formules Latex sont des fois mal interprétées dans ce message, pourtant elles me semblent correctement écrites.
-----

[geometrodynamics_of_QFT]

Bonjour,

Je ne sais pas si ça peut aider, mais il me semble que la dérivée covariante d'un vecteur contravariant soit un tenseur, par conséquent il lui faut deux indices...
Enfin, je m'embrouille peut-être, mais au lieu de :


j'écrirais plutôt :



ça ressemble plus à une dérivée totale non?
Désolé si je suis à côté de la plaque...

[fabio123]

en fait, les équations (1) et (2) s'obtiennent en multipliant l'expression de la dérivée covariante par .

La dérivée covariante s'écrit :



et je multiplie (1) par dy^{i} pour obtenir :

[fabio123]

Je dois préciser que j'arrive grâce à mon programme à bien reproduire le transport d'un vecteur le long d'un "grand cercle" (une géodésique) : ceci est grâce à un algorithme et j'aimerais maintenant pouvoir le vérifier d'un point de vue numérique.

Voici par exemple une figure montrant les valeurs obtenues pour les équations (1) et (2) (si j'additionne tous leurs termes, elles devraient être égales toutes les 2 à 0).



Les valeurs pour l'équation (1) (c'est à dire pour la différentielle totale de \theta) correspondent à la courbe bleue : on peut dire qu'elle reste dans un intervalle [-1,1] (j'ai pris un vecteur initial de norme égale à 20); c'est un peu éloigné de la valeur 0 mais je n'ai pas pu faire mieux.

Les valeurs pour l'équation (2) (pour la différentielle totale de \varphi) correspondent à la courbe rouge et là, on est bien loin d'une valeur nulle.

Ces 2 courbes ont été produites en essayant d'intégrer de manière discrète les équations (1) et (2) comme je l'ai précisé dans mon premier message.

Est-ce que la nullité d'une différentielle totale est valable pour des petites variations d\varphi et d\theta ? ou est-ce qu'il faut à tout prix pouvoir intégrer les équations (1) et (2) ? je suis un peu perdu ...

[A voir en vidéo sur Futura]