Bon élément différentiel dans un calcul de volume

[freemp]

Bonjour à tous.

J'ai un "problème" que je ne sais pas expliquer pour un calcul de surface.

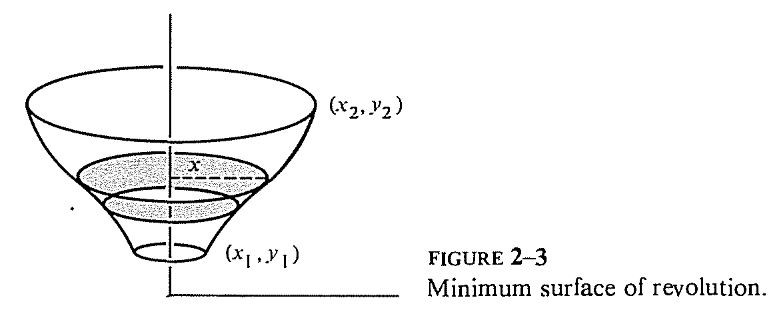
En gros le contexte de l'exo c'est d'appliquer les principes de calculs variationnels permettant de trouver la plus petite surface de révolution reliant un cercle de rayon x1 en y=y1 et un cercle de rayon x2 en y=y2 pour vous donner une idée (même si vous avez pas besoin de savoir ça pour comprendre la question).

Mais le problème que j'ai est le suivant : pour moi, la surface élémentaire en y s'écrit comme :



Mais dans la correction, la surface élémentaire est en fait :

avec

Mais je ne comprends pas en quoi ce que j'ai fait est faux pour autant. Comment je peux savoir que pour bien faire le calcul il faut faire une "interpolation linéaire" entre deux cercles espacés infinitésimalement et pas juste les relier par une droite constante. Ce que je veux dire c'est que ce que j'ai fait consiste implicitement à approximer l'intégrale par des fonctions en escalier, à prendre la limite vers 0 de ces fonctions en escalier (enfin c'est que qui me semble). Et si on se réfère à l'intégrale de Riemann ça suffit non ? (cf https://upload.wikimedia.org/wikiped...wn_Riemann.jpg).

En résumé : comment peut on deviner que le ds à prendre est celui et non pas



Merci beaucoup !
-----

[freemp]

Pour être un peu plus explicite avec mon problème, si je veux calculer l'aire entre deux bornes sous la fonction , j'écrirai :

et pas

Car (c'est comme ça que je le comprends en tout cas), l'intégrale de Riemann est construite avec des fonctions en escalier donc il suffit de multiplier par une largeur infinitésimale dx (c'est très à la physicienne je sais).

C'est un peu le même problème que j'ai avec mon calcul exposé : pourquoi prendre suffit pas, pourquoi il faut prendre ?

Merci beaucoup !

[phys4]

Bonsoir,
L'intégrale indiquée correspond au calcul d'une surface de symétrie cylindrique dont la courbe génératrice à pour équation x(y).
La constante indique que l'on prend le cercle autour de l'axe y et qu'on intègre l'élément de zone cylindrique.

La largeur de la zone n'est pas dx, car cette génératrice est oblique et il faut prendre ds le long de la génératrice.
Ce ne serait pas le cas si l'on voulait calculer le volume de la surface cylindrique.

[freemp]

Oui mais justement comment vous pouvez savoir que pour le volume il faut prendre "dy" et pour la surface "ds". Comment dans un cas général on fait pour savoir quel est le bon élément différentiel à choisir ? Ça me parait pas évident.

Merci.

[A voir en vidéo sur Futura]

[phys4]

Il faut bien se représenter ce que l'on veut calculer: pour cela écrire la surface élémentaire (ou le volume) qu'il faut intégrer. Un dessin peut aider.

Un peu d'intuition physique, et l'habitude de la géométrie dans l'espace sont des atouts à acquérir.

[freemp]

Je sais pas si c'est une question de représentation dans l'espace ou pas mais par exemple pour moi à part changer 2*pi*r(y) en pi*r(y)^2, le calcul de la surface et du volume de révolution devraient être les mêmes.

Or pour le volume on prend dy et pour la surface ds.

Ça reste assez obscur pour moi cette différence d'élément différentiel entre le volume et la surface ici, par exemple.

Je sais pas quoi dire à part : avez vous une explication plus détaillée ?

[phys4]

Pour le volume vous avez un disque, son volume dépend de son rayon et de l'épaisseur, ici l'élément différentiel est l'épaisseur, le fait que le bord soit oblique n'intervient pas sur le volume.

Pour la surface, vous avez un tronc de cône, sa surface est le produit de la longueur du cercle par la longueur le long la génératrice, c'est cette longueur l'élément différentiel, voyez vous la différence ?

[freemp]

En admettant connues les méthodes de calcul du volume et de la surface d'un cône je suis totalement d'accord avec vous (en effet pour un cône on prend comme élément différentiel le ds pour la surface et le dz pour le volume, et le problème qu'on a ici est analogue au calcul de volume et de surface d'un cône).

Mais, même si la question peut sembler basique j'avoue que je n'ai jamais compris pourquoi on devait prendre ds pour la surface pour un cône et pas dz comme pour le volume.

En fait pour le volume ça me parait assez logique de prendre dz mais c'est pour la surface que j'ai du mal à voir pourquoi on prend ds.

Désolé c'est peut être évident mais pas pour moi.

[edit] : si ça l'est évident pour le volume c'est parce que je me ramène à un calcul d'intégrale 1D. Quand j’intègre x^2, je calcule l'aire sous la courbe. Et d'un point de vue "géométrique" l'élément différentiel est dx et pas ds car je calcule la surface entre la droite y=0 (donc là où x varie) et x^2. Donc le dx correspond pour moi à une largeur infinitésimale d'une fonction en escalier en gros ( https://upload.wikimedia.org/wikiped...wn_Riemann.jpg ).
Mais pour le calcul de la surface de révolution j'arrive pas à me ramener à ça.

[Médiat]

Bonjour Essayez de visualiser l'erreur quand on prend dy au lieu de ds dans le cas du volume (négligeable ) et dans le cas de la surface (énorme)

Les mêmes questions de posent en 2D, entre le calcul de surface sous la courbe et le calcul de la longueur de la courbe

[gg0]

Bonjour freemp.

Pour obtenir un volume, il faut intégrer des éléments de volumes; pour obtenir une surface, intégrer des éléments de surface. Pour le volume, des éléments du volume qu'on veut, pour une surface, des éléments de la surface qu'on veut.
Comme on est dans "l'infiniment petit", les éléments de volumes s'approximent par des formes simples (parallélépipèdes, cylindres,...) et les éléments de surface aussi (disques, rectangles, troncs de cônes, ...).

Manifestement, vu tes messages, tu cherchais une écriture commune ,alors que ce qui est nécessaire, c'est la compréhension de ce qui est calculé. Et les détails te cachent la méthode :
"je n'ai jamais compris pourquoi on devait prendre ds pour la surface pour un cône et pas dz comme pour le volume." Moi non plus, car on ne prend pas dz pour le volume, mais dv où v est le volume. Puis on calcule dv en fonction de différentes variables : 3 si on utilise une intégrale triple, une seule, z par exemple, si on arrive à se ramener à une seule variable, comme dans les volumes de révolution : pi f(z)²dz =dv.

Cordialement.

[freemp]

Bonjour à tous.

Merci pour vos réponses.

Je pense avoir compris mais j'aimerai avoir une confirmation.

Pour l'histoire du volume, le volume infinitésimal est bien : parce que si on ajoute les termes supplémentaires ils sont négligeables.

Concrètement on aurait

En effet, le terme supplémentaire en vient du triangle qui se rajoute si on considère le fait que r dépend de y (j'avoue qu'un schéma serait pas mal mais j’espère que vous visualisez ce dont je parle). Mais comme c'est un terme d'ordre 2 en il donnera une contribution nulle pour l'intégrale de Riemann.

Donc on a bien uniquement à l'ordre 1.

Pour la surface en revanche, on a directement:



Là on pourrait se dire "oui mais comme , il varie sur la surface infinitésimale", mais d'après la construction de l'intégrale de Riemann, on calcule l'intégrale en prenant la limite avec les fonctions constantes par morceaux, donc on suppose que le long du ds, la grandeur à intégrer ne varie pas (car c'est comme ça que l'intégrale est construite).

Et un petit supplément pour être sur avec un exemple d'intégrale en 1D :

Supposons que je veuille intégrer la fonction pour calculer l'aire sous la courbe. (Evidemment l'aire sera , mais je cherche à faire une rapide justification géométrique en utilisant la construction de Riemann).

En gros je trace ma fonction et j'essaie de l'approcher par des fonctions linéaires (donc pas par des fonctions constantes par morceaux).

J'aurai donc l'aire qui sera :

Le second terme vient du fait que j'ai un triangle qui se rajoute au dessus de mon approximation par fonctions constantes par morceaux.

Si je traduis cela en série, ça me dit que mon intégrale vaut :



Le deuxième terme donnera une contribution nulle car prendre la valeur de f à gauche ou à droite changera pas la somme pour la limite N->inf, c'est dans ce cas précis une autre manière de dire que les termes d'ordre 2 en dx donnent une contribution nulle à l'intégrale.

Est ce que ma justification mi maths-mi physique est la bonne ?

D'ailleurs c'est un peu comme ça qu'on peut donner un sens aux dx, dy. Pour bien comprendre leur sens il faut se ramener à la série qui définit l'intégrale, ça correspond à la largeur de la fonction constante par morceaux qui approxime l'intégrale avant le passage à la limite. Êtes vous d'accord avec ceci ? Car c'est un truc qui m'a toujours un peu intrigué cette notation de dx "une petite largeur", ça me paraissait assez flou mais j'ai l'impression que ça correspond précisément à la largeur de la fonction continue par morceaux avant le passage à la limite ?

Merci beaucoup !

[gg0]

Si ça te permet une intuition correcte, pourquoi pas. Leibnitz raisonnait en termes de quantités "évanouissantes", Euler aussi, puis on a rationalisé ça avec la notion de limite et l'intégrale de Riemann, et on définit plus les volumes et les surfaces comme des résultats d'intégrales que le contraire. Ces intégrales étant justement celles que tu rencontres.
En général, on ne parle même pas de tes "petits triangles", car quand on passe de x à x+dx, les quantités ne varient pas vraiment, dx étant infiniment petit.

Cordialement.

[freemp]

Ok, merci beaucoup