Bonsoir,
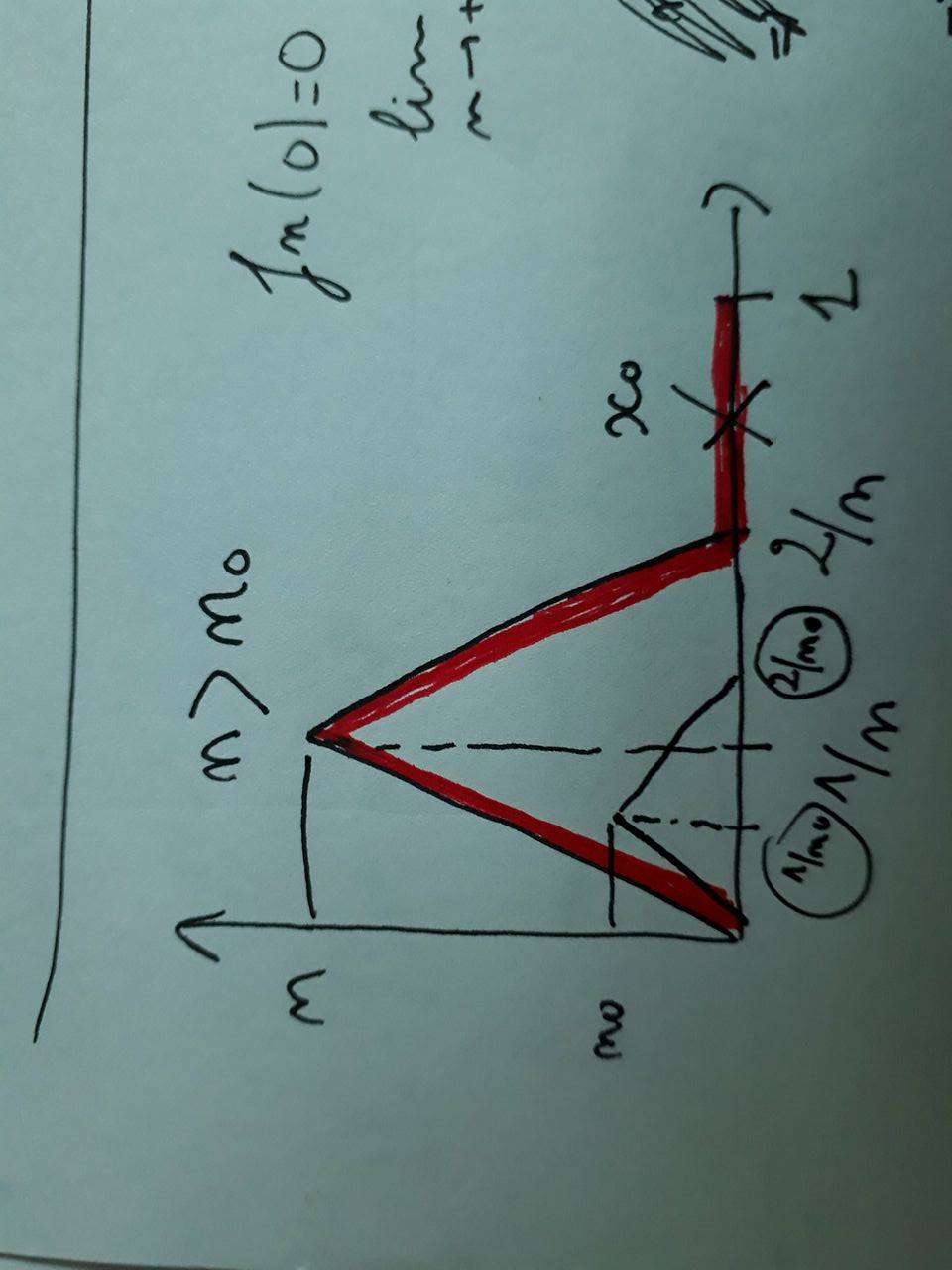
Soit fn la suite de fonction définie sur [0,1] paret
Déjà je comprends pas l'intérêt de la suite j'arrive pas à la représenter.
1/ Montrer que fn converge simplement mais pas uniformément vers une fonction f sur [0,1] de sorte que la suite de réels :
J'ai rien compris
Déjà avec un énoncé correct, ça serrait mieux. Tes fonctions sont définies sur [0,1] mais tu écris f(n)?
Oui désolé :Envoyé par Tryss2
soit fn définie et continue sur [0,1] par :
Etudier la convergence simple et uniforme. Calculer l'intégrale entre 0 et 1 de fn(x).
Ce que j'ai fait :
Alors,
Sinon j'ai fait un dessin ci dessous avec un n0 > n :
Soit x0 dans ]0,1],
Si
On a montré :
Enfin :
On a ainsi montré la convergence simple de la suite de fonction (fn)
Pour la convergence uniforme faut étudier :
Le sup est égal au Max car on voit que la borne Sup est atteinte...
Graphiquement je trouve n, mais je sais pas comment le démontrer rigoureusement. Comme dois je procéder ?
Heu ... étudier une fonction se fait au lycée, et le tableau de variations donne le résultat.
En plus, pour une fonction affine par morceaux, le niveau seconde suffit.
Bon travail !
En effet, je fais la dérivée et le tableau de variation de trouve bien 1/n !
